ANOTHER JOINER'S PROBLEM.—solution

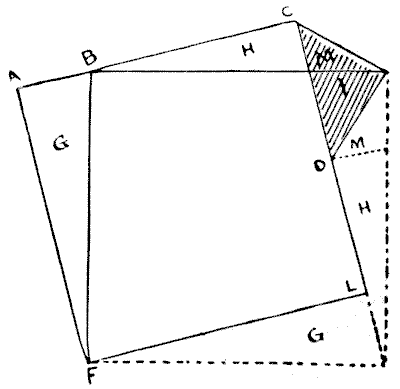
The point was to find a general rule for forming a perfect square out of another square combined with a "right-angled isosceles triangle." The triangle to which geometricians give this high-sounding name is, of course, nothing more or less than half a square that has been divided from corner to corner.
The precise relative proportions of the square and triangle are of no consequence whatever. Pg 172It is only necessary to cut the wood or material into five pieces.
Suppose our original square to be ACLF in the above diagram and our triangle to be the shaded portion CED. Now, we first find half the length of the long side of the triangle (CD) and measure off this length at AB. Then we place the triangle in its present position against the square and make two cuts—one from B to F, and the other from B to E. Strange as it may seem, that is all that is necessary! If we now remove the pieces G, H, and M to their new places, as shown in the diagram, we get the perfect square BEKF.
Take any two square pieces of paper, of different sizes but perfect squares, and cut the smaller one in half from corner to corner. Now proceed in the manner shown, and you will find that the two pieces may be combined to form a larger square by making these two simple cuts, and that no piece will be required to be turned over.
The remark that the triangle might be "a little larger or a good deal smaller in proportion" was intended to bar cases where area of triangle is greater than area of square. In such cases six pieces are necessary, and if triangle and square are of equal area there is an obvious solution in three pieces, by simply cutting the square in half diagonally.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org