THE PENTAGON AND SQUARE.—solution

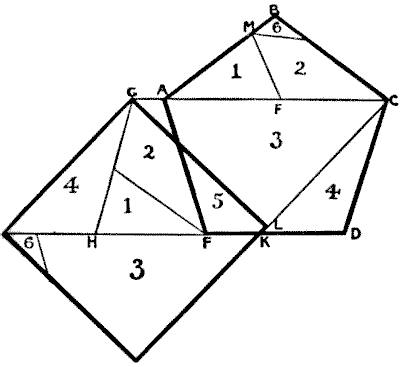
A regular pentagon may be cut into as few as six pieces that will fit together without any turning over and form a square, as I shall show below. Hitherto the best answer has been in seven pieces—the solution produced some years ago by a foreign mathematician, Paul Busschop. We first form a parallelogram, and from that the square. The process will be seen in the diagram on the next page.

The pentagon is ABCDE. By the cut AC and the cut FM (F being the middle point between A and C, and M being the same distance from A as F) we get two pieces that may be placed in position at GHEA and form the parallelogram GHDC. We then find the mean proportional between the length HD and the height of the parallelogram. This distance we mark off from C at K, then draw CK, and from G drop the line GL, perpendicular to KC. The rest is easy and rather obvious. It will be seen that the six pieces will form either the pentagon or the square.

I have received what purported to be a solution in five pieces, but the method was based on the rather subtle fallacy that half the diagonal plus half the side of a pentagon equals the side of a square of the same area. I say subtle, because it is an extremely close approximation that will deceive the eye, and is quite difficult to prove inexact. I am not aware that attention has before been drawn to this curious approximation.

Another correspondent made the side of his square 1¼ of the side of the pentagon. As a matter of fact, the ratio is irrational. I calculate that if the side of the pentagon is 1—inch, foot, or anything else—the side of the square of equal area is 1.3117 nearly, or say roughly 1³/₁₀. So we can only hope to solve the puzzle by geometrical methods.

click here to go to my blog.

See more interesting puzzles at http://puzzles.50webs.org