THE YORKSHIRE ESTATES.—solution
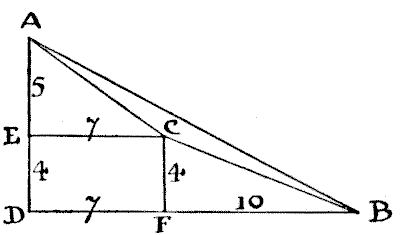
The triangular piece of land that was not for sale contains exactly eleven acres. Of course it is not difficult to find the answer if we follow the eccentric and tricky tracks of intricate trigonometry; or I might say that the application of a well-known formula reduces the problem to finding one-quarter of the square root of (4 × 370 × 116) - (370 + 116 - 74)²—that is a quarter of the square root of 1936, which is one-quarter of 44, or 11 acres. But all that the reader really requires to know is the Pythagorean law on which many puzzles have been built, that in any right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. I shall dispense with all "surds" and similar absurdities, notwithstanding the fact that the sides of our triangle are clearly incommensurate, since we cannot exactly extract the square roots of the three square areas.

In the above diagram ABC represents our triangle. ADB is a right-angled triangle, AD measuring 9 and BD measuring 17, because the square of 9 added to the square of 17 equals 370, the known area of the square on AB. Also AEC is a right-angled triangle, and the square of 5 added to the square of 7 equals 74, the square estate on A C. Similarly, CFB is a right-angled triangle, for the square of 4 added to the square of 10 equals 116, the square estate on BC. Now, although the sides of our triangular estate are incommensurate, we have in this diagram all the exact figures that we need to discover the area with precision.
The area of our triangle ADB is clearly half of 9 × 17, or 76½ acres. The area of AEC is half of 5 × 7, or 17½ acres; the area of CFB is half of 4 × 10, or 20 acres; and the area of the oblong EDFC is obviously 4 × 7, or 28 acres. Now, if we add together 17½, 20, and 28 = 65½, and deduct this sum from the area of the large triangle ADB (which we have found to be 76½ acres), what remains must clearly be the area of ABC. That is to say, the area we want must be 76½ - 65½ = 11 acres exactly.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org