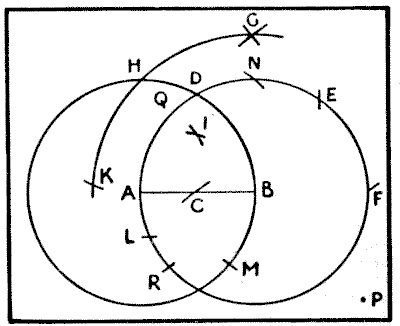
THE COMPASSES PUZZLE.—solution

Let AB in the following diagram be the given straight line. With the centres A and B and radius AB describe the two circles. Mark off DE and EF equal to AD. With the centres A and F and radius DF describe arcs intersecting at G. With the centres A and B and distance BG describe arcs GHK and N. Make HK equal to AB and HL equal to HB. Then with centres K and L and radius AB describe arcs intersecting at I. Make BM equal to BI. Finally, with the centre M and radius MB cut the line in C, and the point C is the required middle of the line AB. For greater exactitude you can mark off R from A (as you did M from B), and from R describe another arc at C. This also solves the problem, to find a point midway between two given points without the straight line.

I will put the young geometer in the way of a rigid proof. First prove that twice the square of the line AB equals the square of the distance BG, from which it follows that HABN are the four corners of a square. To prove that I is the centre of this square, draw a line from H to P through QIB and continue the arc HK to P. Then, conceiving the necessary lines to be drawn, the angle HKP, being in a semicircle, is a right angle. Let fall the perpendicular KQ, and by similar triangles, and from the fact that HKI is an isosceles triangle by the construction, it can be proved that HI is half of HB. We can similarly prove that C is the centre of the square of which AIB are three corners.

I am aware that this is not the simplest possible solution.

click here to go to my blog.

See more interesting puzzles at http://puzzles.50webs.org