A KITE-FLYING PUZZLE.—solution

Solvers of this little puzzle, I have generally found, may be roughly divided into two classes: those who get within a mile of the correct answer by means of more or less complex calculations, involving "pi," and those whose arithmetical kites fly hundreds and thousands of miles away from the truth. The comparatively easy method that I shall show does not involve any consideration of the ratio that the diameter of a circle bears to its circumference. I call it the "hat-box method."

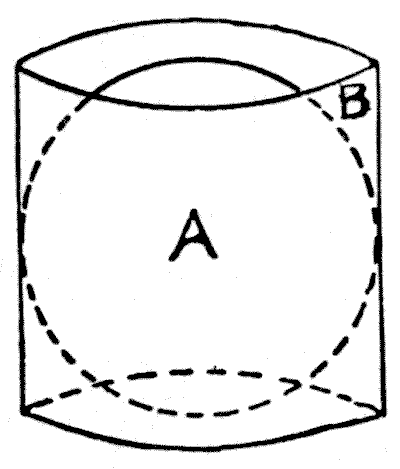
Supposing we place our ball of wire, A, in a cylindrical hat-box, B, that exactly fits it, so that it touches the side all round and exactly touches the top and bottom, as shown in the illustration. Then, by an invariable law that should be known by everybody, that box contains exactly half as much again as the ball. Therefore, as the ball is 24 in. in diameter, a hat-box of the same circumference but two-thirds of the height (that is, 16 in. high) will have exactly the same contents as the ball.

Now let us consider that this reduced hat-box is a cylinder of metal made up of an immense number of little wire cylinders close together like the hairs in a painter's brush. By the conditions of the puzzle we are allowed to consider that there are no spaces between the wires. How many of these cylinders one one-hundredth of an inch thick are equal to the large cylinder, which is 24 in. thick? Circles are to one another as the squares of their diameters. The square of ¹/₁₀₀ is ¹/₁₀₀₀₀₀, and the square of 24 is 576; therefore the large cylinder contains 5,760,000 of the little wire cylinders. But we have seen that each of these wires is 16 in. long; hence 16 × 5,760,000 = 92,160,000 inches as the complete length of the wire. Reduce this to miles, and we get 1,454 miles 2,880 ft. as the length of the wire attached to the professor's kite.

Whether a kite would fly at such a height, or support such a weight, are questions that do not enter into the problem.

click here to go to my blog.

See more interesting puzzles at http://puzzles.50webs.org