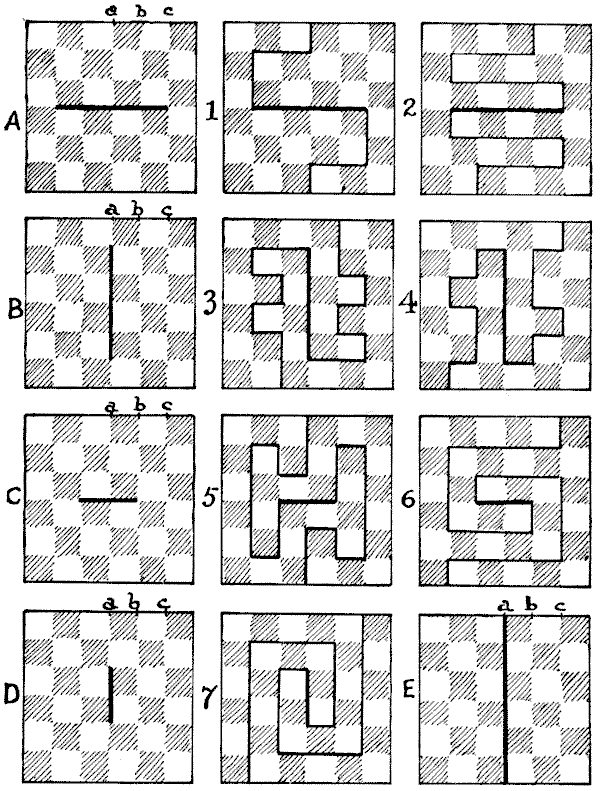
CHEQUERED BOARD DIVISIONS.—solution
There are 255 different ways of cutting the board into two pieces of exactly the same size and shape. Every way must involve one of the five cuts shown in Diagrams A, B, C, D, and E. To avoid repetitions by reversal and reflection, we need only consider cuts that enter at the points a, b, and c. But the exit must always be at a point in a straight line from the entry through the centre. This is the most important condition to remember. In case B you cannot enter at a, or you will get the cut provided for in E. Similarly in C or D, you must not enter the key-line in the same direction as itself, or you will get A or B. If you are working on A or C and entering at a, you must consider joins at one end only of the key-line, or you will get repetitions. In other cases you must consider joins at both ends of the key; but after leaving a in case D, turn always either to right or left—use one direction only. Figs. 1 and 2 are examples under A; 3 and 4 are examples under B; 5 and 6 come under C; and 7 is a pretty example of D. Of course, E is a peculiar type, and obviously admits of only one way of cutting, for you clearly cannot enter at b or c.

Here is a table of the results:—
| a | b | c | Ways. | |||||
| A | = | 8 | + | 17 | + | 21 | = | 46 |
| B | = | 0 | + | 17 | + | 21 | = | 38 |
| C | = | 15 | + | 31 | + | 39 | = | 85 |
| D | = | 17 | + | 29 | + | 39 | = | 85 |
| E | = | 1 | + | 0 | + | 0 | = | 1 |
| 41 | 94 | 120 | 255 |
I have not attempted the task of enumerating the ways of dividing a board 8x8—that is, an ordinary chessboard. Whatever the method adopted, the solution would entail considerable labour.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org