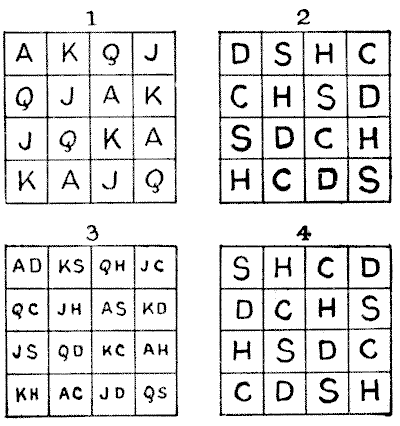
BACHET'S SQUARE.—solution

Let us use the letters A, K, Q, J, to denote ace, king, queen, jack; and D, S, H, C, to denote diamonds, spades, hearts, clubs. In Diagrams 1 and 2 we have the two available ways of arranging either group of letters so that no two similar letters shall be in line—though a quarter-turn of 1 will give us the arrangement in 2. If we superimpose or combine these two squares, we get the arrangement of Diagram 3, which is one solution. But in each square we may put the letters in the top line in twenty-four different ways without altering the scheme of arrangement. Thus, in Diagram 4 the S's are similarly placed to the D's in 2, the H's to the S's, the C's to the H's, and the D's to the C's. It clearly follows that there must be 24 × 24 = 576 ways of combining the two primitive arrangements. But the error that Labosne fell into was that of assuming that the A, K, Q, J must be arranged in the form 1, and the D, S, H, C in the form 2. He thus included reflections and half-turns, but not quarter-turns. They may obviously be interchanged. So that the correct answer is 2 × 576 = 1,152, counting reflections and reversals as different. Put in another manner, the pairs in the top row may be written in 16 × 9 ×4 × 1 = 576 different ways, and the square then completed in 2 ways, making 1,152 ways in all.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org