THE KENNEL PUZZLE.—solution

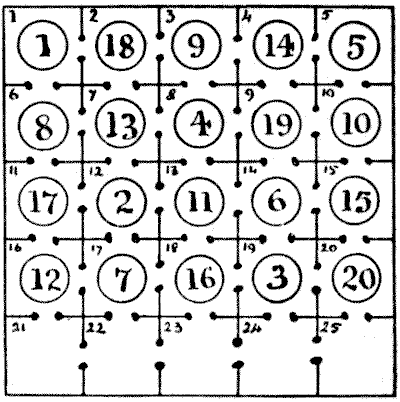
The first point is to make a choice of the most promising knight's string and then consider the question of reaching the arrangement in the fewest moves. I am strongly of opinion that the best string is the one represented in the following diagram, in which it will be seen that each successive number is a knight's move from the preceding one, and that five of the dogs (1, 5, 10, 15, and 20) never leave their original kennels.

This position may be arrived at in as few as forty-six moves, as follows: 16—21, 16—22, 16—23, 17—16, 12—17, 12—22, 12—21,7—12, 7—17, 7—22, 11—12, 11—17, 2—7, 2—12, 6—11, 8—7, 8—6, 13—8, 18—13, 11—18, 2—17, 18—12, 18—7, 18—2, 13—7, 3—8, 3—13, 4—3, 4—8, 9—4, 9—3, 14—9, 14—4, 19—14, 19—9, 3—14, 3—19, 6—12, 6—13, 6—14, 17—11, 12—16, 2—12, 7—17, 11—13, 16—18 = 46 moves. I am, of course, not able to say positively that a solution cannot be discovered in fewer moves, but I believe it will be found a very hard task to reduce the number.

click here to go to my blog.

See more interesting puzzles at http://puzzles.50webs.org