THE SIX PAWNS.—solution
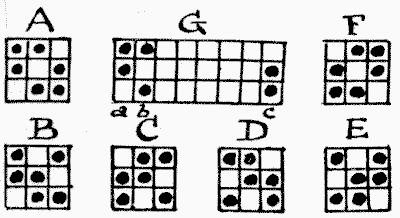
The general formula for six pawns on all squares greater than 22 is this: Six times the square of the number of combinations of n things taken three at a time, where n represents the number of squares on the side of the board. Of course, where n is even the unoccupied squares in the rows and columns will be even, and where n is odd the number of squares will be odd. Here n is 8, so the answer is 18,816 different ways. This is "The Dyer's Puzzle" (Canterbury Puzzles, No. 27) in another form. I repeat it here in order to explain a method of solving that will be readily grasped by the novice. First of all, it is evident that if we put a pawn on any line, we must put a second one in that line in order that the remainder may be even in number. We cannot put four or six in any row without making it impossible to get an even number in all the columns interfered with. We have, therefore, to put two pawns in each of three rows and in each of three columns. Now, there are just six schemes or arrangements that fulfil these conditions, and these are shown in Diagrams A to F, inclusive, on next page.

I will just remark in passing that A and B are the only distinctive arrangements, because, if you give A a quarter-turn, you get F; and if you give B three quarter-turns in the direction that a clock hand moves, you will get successively C, D, and E. No matter how you may place your six pawns, if you have complied with the conditions of the puzzle they will fall under one of these arrangements. Of course it will be understood that mere expansions do not destroy the essential character of the arrangements. Thus G is only an expansion of form A. The solution therefore consists in finding the number of these expansions. Supposing we confine our operations to the first three rows, as in G, then with the pairs a and b placed in the first and second columns the pair c may be disposed in any one of the remaining six columns, and so give six solutions. Now slide pair b into the third column, and there are five possible positions for c. Slide b into the fourth column, and c may produce four new solutions. And so on, until (still leaving a in the first column) you have b in the seventh column, and there is only one place for c—in the eighth column. Then you may put a in the second column, b in the third, and c in the fourth, and start sliding c and b as before for another series of solutions.
We find thus that, by using form A alone and confining our operations to the three top rows, we get as many answers as there are combinations of 8 things taken 3 at a time. This is (8 × 7 × 6)/(1 × 2 × 3) = 56. And it will at once strike the reader that if there are 56 different ways of electing the columns, there must be for each of these ways just 56 ways of selecting the rows, for we may simultaneously work that "sliding" process downwards to the very bottom in exactly the same way as we have worked from left to right. Therefore the total number of ways in which form A may be applied is 56 × 6 = 3,136. But there are, as we have seen, six arrangements, and we have only dealt with one of these, A. We must, therefore, multiply this result by 6, which gives us 3,136 × 6 = 18,816, which is the total number of ways, as we have already stated.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org