MAGIC SQUARES OF TWO DEGREES.—solution
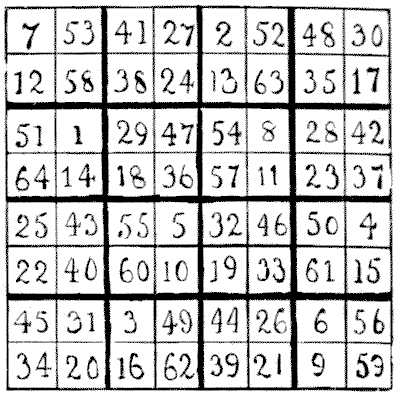
The following is the square that I constructed. As it stands the constant is 260. If for every number you substitute, in its allotted place, its square, then the constant will be 11,180. Readers can write out for themselves the second degree square.

The main key to the solution is the pretty law that if eight numbers sum to 260 and their squares to 11,180, then the same will happen in the case of the eight numbers that are complementary to 65. Thus 1 + 18 + 23 + 26 + 31 + 48 + 56 + 57 = 260, and the sum of their squares is 11,180. Therefore 64 + 47 + 42 + 39 + 34 + 17 + 9 + 8 (obtained by subtracting each of the above numbers from 65) will sum to 260 and their squares to 11,180. Note that in every one of the sixteen smaller squares the two diagonals sum to 65. There are four columns and four rows with their complementary columns and rows. Let us pick out the numbers found in the 2nd, 1st, 4th, and 3rd rows and arrange them thus :—
| 1 | 8 | 28 | 29 | 42 | 47 | 51 | 54 |
| 2 | 7 | 27 | 30 | 41 | 48 | 52 | 53 |
| 3 | 6 | 26 | 31 | 44 | 45 | 49 | 56 |
| 4 | 5 | 25 | 32 | 43 | 46 | 50 | 55 |
Here each column contains four consecutive numbers cyclically arranged, four running in one direction and four in the other. The numbers in the 2nd, 5th, 3rd, and 8th columns of the square may be similarly grouped. The great difficulty lies in discovering the conditions governing these groups of numbers, the pairing of the complementaries in the squares of four and the formation of the diagonals. But when a correct solution is shown, as above, it discloses all the more important keys to the mystery. I am inclined to think this square of two degrees the most elegant thing that exists in magics. I believe such a magic square cannot be constructed in the case of any order lower than 8.
click here to go to my blog.
See more interesting puzzles at http://puzzles.50webs.org