Puzzles to puzzle you

This is a very ancient branch of mathematical puzzledom, and it has an immense, though scattered, literature of its own. In their simple form of consecutive whole numbers arranged in a square so that every column, every row, and each of the two long diagonals shall add up alike, these magic squares offer three main lines of investigation: Construction, Enumeration, and Classification. Of recent years many ingenious methods have been devised for the construction of magics, and the law of their formation is so well understood that all the ancient mystery has evaporated and there is no longer any difficulty in making squares of any dimensions. Almost the last word has been said on this subject. The question of the enumeration of all the possible squares of a given order stands just where it did over two hundred years ago. Everybody knows that there is only one solution for the third order, three cells by three; and Frénicle published in 1693 diagrams of all the arrangements of the fourth order—880 in number—and his results have been verified over and over again. I may here refer to the general solution for this order, for numbers not necessarily consecutive, by E. Bergholt in Nature, May 26, 1910, as it is of the greatest importance to students of this subject. The enumeration of the examples of any higher order is a completely unsolved problem.

As to classification, it is largely a matter of individual taste—perhaps an æsthetic question, for there is beauty in the law and order of numbers. A man once said that he divided the human race into two great classes: those who take snuff and those who do not. I am not sure that some of our classifications of magic squares are not almost as valueless. However, lovers of these things seem somewhat agreed that Nasik magic squares (so named by Mr. Frost, a student of them, after the town in India where he lived, and also called Diabolique and Pandiagonal) and Associated magic squares are of special interest, so I will just explain what these are for the benefit of the novice.

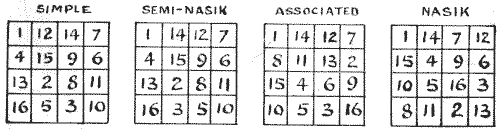
I published in The Queen for January 15, 1910, an article that would enable the reader to write out, if he so desired, all the 880 magics of the fourth order, and the following is the complete classification that I gave. The first example is that of a Simple square that fulfils the simple conditions and no more. The second example is a Semi-Nasik, which has the additional property that the opposite short diagonals of two cells each together sum to 34. Thus, 14 + 4 + 11 + 5 = 34 and 12 + 6 + 13 + 3 = 34. The third example is not only Semi-Nasik but also Associated, because in it every number, if added to the number that is equidistant, in a straight line, from the centre gives 17. Thus, 1 + 16, 2 + 15, 3 + 14, etc. The fourth example, considered the most "perfect" of all, is a Nasik. Here all the broken diagonals sum to 34. Thus, for example, 15 + 14 + 2 + 3, and 10 + 4 + 7 + 13, and 15 + 5 + 2 + 12. As a consequence, its properties are such that if you repeat the square in all directions you may mark off a square, 4 × 4, wherever you please, and it will be magic.

The following table not only gives a complete enumeration under the four forms described, but also a classification under the twelve graphic types indicated in the diagrams. The dots at the end of each line represent the relative positions of those complementary pairs, 1 + 16, 2 + 15, etc., which sum to 17. For example, it will be seen that the first and second magic squares given are of Type VI., that the third square is of Type III., and that the fourth is of Type I. Edouard Lucas indicated these types, but he dropped exactly half of them and did not attempt the classification.

NASIK	(Type I.)			48
SEMI-NASIK	(Type II., Transpositions of Nasik)		48
"	(Type III., Associated)		48
"	(Type IV.)	96
"	(Type V.)	96	192
"	(Type VI.)		96	384
SIMPLE.	(Type VI.)		208
"	(Type VII.)	56
"	(Type VIII.)	56
"	(Type IX.)	56
"	(Type X.)	56	224
"	(Type XI.)	8
"	(Type XII.)	8	16	448
				880

It is hardly necessary to say that every one of these squares will produce seven others by mere reversals and reflections, which we do not count as different. So that there are 7,040 squares of this order, 880 of which are fundamentally different.

An infinite variety of puzzles may be made introducing new conditions into the magic square. In The Canterbury Puzzles I have given examples of such squares with coins, with postage stamps, with cutting-out conditions, and other tricks. I will now give a few variants involving further novel conditions.

Nearly everybody knows that a "magic square" is an arrangement of numbers in the form of a square so that every row, every column, and each of the two long diagonals adds up alike. For example, you would find little difficulty in merely placing a different number in each of the nine cells in the illustration so that the rows, columns, and diagonals shall all add up 15. And at your first attempt you will probably find that you have an 8 in one of the corners. The puzzle is to construct the magic square, under the same conditions, with the 8 in the position shown.

I happened to have lying on my table a number of strips of cardboard, with numbers printed on them from 1 upwards in numerical order. The idea suddenly came to me, as ideas have a way of unexpectedly coming, to make a little puzzle of this. I wonder whether many readers will arrive at the same solution that I did.

Take seven strips of cardboard and lay them together as above. Then write on each of them the numbers 1, 2, 3, 4, 5, 6, 7, as shown, so that the numbers shall form seven rows and seven columns.

Now, the puzzle is to cut these strips into the fewest possible pieces so that they may be placed together and form a magic square, the seven rows, seven columns, and two diagonals adding up the same number. No figures may be turned upside down or placed on their sides—that is, all the strips must lie in their original direction.

Of course you could cut each strip into seven separate pieces, each piece containing a number, and the puzzle would then be very easy, but I need hardly say that forty-nine pieces is a long way from being the fewest possible.

The illustration shows the plan of a prison of nine cells all communicating with one another by doorways. The eight prisoners have their numbers on their backs, and any one of them is allowed to exercise himself in whichever cell may happen to be vacant, subject to the rule that at no time shall two prisoners be in the same cell. The merry monarch in whose dominions the prison was situated offered them special comforts one Christmas Eve if, without breaking that rule, they could so place themselves that their numbers should form a magic square.

Now, prisoner No. 7 happened to know a good deal about magic squares, so he worked out a scheme and naturally selected the method that was most expeditious—that is, one involving the fewest possible moves from cell to cell. But one man was a surly, obstinate fellow (quite unfit for the society of his jovial companions), and he refused to move out of his cell or take any part in the proceedings. But No. 7 was quite equal to the emergency, and found that he could still do what was required in the fewest possible moves without troubling the brute to leave his cell. The puzzle is to show how he did it and, incidentally, to discover which prisoner was so stupidly obstinate. Can you find the fellow?

Shortly after the episode recorded in the last puzzle occurred, a ninth prisoner was placed in the vacant cell, and the merry monarch then offered them all complete liberty on the following strange conditions. They were required so to rearrange themselves in the cells that their numbers formed a magic square without their movements causing any two of them ever to be in the same cell together, except that at the start one man was allowed to be placed on the shoulders of another man, and thus add their numbers together, and move as one man. For example, No. 8 might be placed on the shoulders of No. 2, and then they would move about together as 10. The reader should seek first to solve the puzzle in the fewest possible moves, and then see that the man who is burdened has the least possible amount of work to do.

Not fifty miles from Cadiz stood in the middle ages a castle, all traces of which have for centuries disappeared. Among other interesting features, this castle contained a particularly unpleasant dungeon divided into sixteen cells, all communicating with one another, as shown in the illustration.

Now, the governor was a merry wight, and very fond of puzzles withal. One day he went to the dungeon and said to the prisoners, "By my halidame!" (or its equivalent in Spanish) "you shall all be set free if you can solve this puzzle. You must so arrange yourselves in the sixteen cells that the numbers on your backs shall form a magic square in which every column, every row, and each of the two diagonals shall add up the same. Only remember this: that in no case may two of you ever be together in the same cell."

One of the prisoners, after working at the problem for two or three days, with a piece of chalk, undertook to obtain the liberty of himself and his fellow-prisoners if they would follow his directions and move through the doorway from cell to cell in the order in which he should call out their numbers.

He succeeded in his attempt, and, what is more remarkable, it would seem from the account of his method recorded in the ancient manuscript lying before me, that he did so in the fewest possible moves. The reader is asked to show what these moves were.

The above is a trustworthy plan of a certain Russian prison in Siberia. All the cells are numbered, and the prisoners are numbered the same as the cells they occupy. The prison diet is so fattening that these political prisoners are in perpetual fear lest, should their pardon arrive, they might not be able to squeeze themselves through the narrow doorways and get out. And of course it would be an unreasonable thing to ask any government to pull down the walls of a prison just to liberate the prisoners, however innocent they might be. Therefore these men take all the healthy exercise they can in order to retard their increasing obesity, and one of their recreations will serve to furnish us with the following puzzle.

Show, in the fewest possible moves, how the sixteen men may form themselves into a magic square, so that the numbers on their backs shall add up the same in each of the four columns, four rows, and two diagonals without two prisoners having been at any time in the same cell together. I had better say, for the information of those who have not yet been made acquainted with these places, that it is a peculiarity of prisons that you are not allowed to go outside their walls. Any prisoner may go any distance that is possible in a single move.

Take an ordinary pack of cards and throw out the twelve court cards. Now, with nine of the remainder (different suits are of no consequence) form the above magic square. It will be seen that the pips add up fifteen in every row in every column, and in each of the two long diagonals. The puzzle is with the remaining cards (without disturbing this arrangement) to form three more such magic squares, so that each of the four shall add up to a different sum. There will, of course, be four cards in the reduced pack that will not be used. These four may be any that you choose. It is not a difficult puzzle, but requires just a little thought.

The illustration shows eighteen dominoes arranged in the form of a square so that the pips in every one of the six columns, six rows, and two long diagonals add up 13. This is the smallest summation possible with any selection of dominoes from an ordinary box of twenty-eight. The greatest possible summation is 23, and a solution for this number may be easily obtained by substituting for every number its complement to 6. Thus for every blank substitute a 6, for every 1 a 5, for every 2 a 4, for 3 a 3, for 4 a 2, for 5 a 1, and for 6 a blank. But the puzzle is to make a selection of eighteen dominoes and arrange them (in exactly the form shown) so that the summations shall be 18 in all the fourteen directions mentioned.

MAGIC SQUARE PROBLEMS.