|
MAZES
AND HOW TO THREAD THEM.
"In wandering mazes lost."
Paradise Lost.
The Old English word "maze," signifying a labyrinth, probably comes from the
Scandinavian, but its origin is somewhat uncertain. The late Professor Skeat
thought that the substantive was derived from the verb, and as in old times to
be mazed or amazed was to be "lost in thought," the transition to a maze in
whose tortuous windings we are lost is natural and easy.
The word "labyrinth" is derived from a Greek word signifying the passages of
a mine. The ancient mines of Greece and elsewhere inspired fear and awe on
account of their darkness and the danger of getting lost in their intricate
passages. Legend was afterwards built round these mazes. The most familiar
instance is the labyrinth made by Dædalus in Crete for King Minos. In the centre
was placed the Minotaur, and no one who entered could find his way out again,
but became the prey of the monster. Seven youths and seven maidens were sent
regularly by the Athenians, and were duly devoured, until Theseus slew the
monster and escaped from the maze by aid of the clue of thread provided by
Ariadne; which accounts for our using to-day the expression "threading a
maze."
The various forms of construction of mazes include complicated ranges of
caverns, architectural labyrinths, or sepulchral buildings, tortuous devices
indicated by coloured marbles and tiled pavements, winding paths cut in the
turf, and topiary mazes formed by clipped hedges. As a matter of fact, they may
be said to have descended to us in precisely this order of variety.
Mazes were used as ornaments on the state robes of Christian emperors before
the ninth century, and were soon adopted in the decoration of cathedrals and
other churches. The original idea was doubtless to employ them as symbols of the
complicated folds of sin by which man is surrounded. They began to abound in the
early part of the twelfth century, and I give an illustration of one of this
period in the parish church at St. Quentin (Fig. 1). It formed a pavement of the
nave, and its diameter is 34½ feet. The path here is the line itself. If you
place your pencil at the point A and ignore the enclosing line, the line leads
you to the centre by a long route over the entire area; but you never have any
option as to direction during your course. As we shall find in similar cases,
these early ecclesiastical mazes were generally not of a puzzle nature, but
simply long, winding paths that took you over practically all the ground
enclosed.
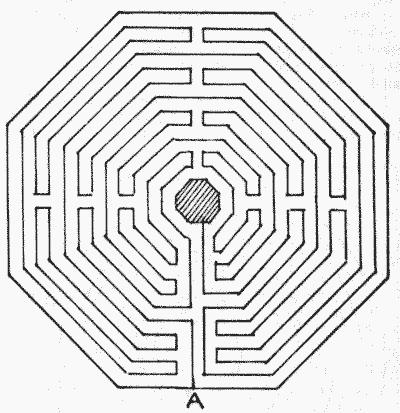 FIG. 1.—Maze at St. Quentin. FIG. 1.—Maze at St. Quentin.
In the abbey church of St. Berlin, at St. Omer, is another of these curious
floors, representing the Temple of Jerusalem, with stations for pilgrims. These
mazes were actually visited and traversed by them as a compromise for not going
to the Holy Land in fulfilment of a vow. They were also used as a means of
penance, the penitent frequently being directed to go the whole course of the
maze on hands and knees.
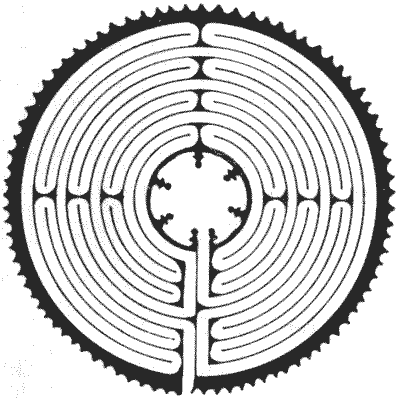 FIG. 2.—Maze in Chartres Cathedral. FIG. 2.—Maze in Chartres Cathedral.
The maze in Chartres Cathedral, of which I give an illustration (Fig. 2), is
40 feet across, and was used by penitents following the procession of Calvary. A
labyrinth in Amiens Cathedral was octagonal, similar to that at St. Quentin,
measuring 42 feet across. It bore the date 1288, but was destroyed in 1708. In
the chapter-house at Bayeux is a labyrinth formed of tiles, red, black, and
encaustic, with a pattern of brown and yellow. Dr. Ducarel, in his "Tour
through Part of Normandy" (printed in 1767), mentions the floor of the great
guard-chamber in the abbey of St. Stephen, at Caen, "the middle whereof
represents a maze or labyrinth about 10 feet diameter, and so artfully contrived
that, were we to suppose a man following all the intricate meanders of its
volutes, he could not travel less than a mile before he got from one end to the
other."
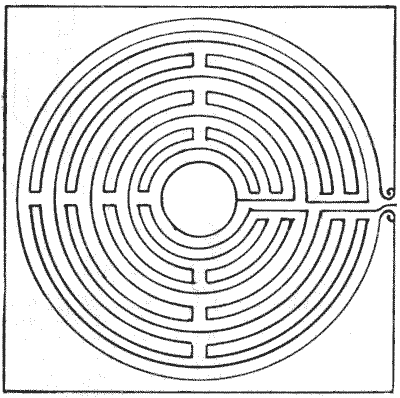 FIG. 3.—Maze in Lucca Cathedral. FIG. 3.—Maze in Lucca Cathedral.
Then these mazes were sometimes reduced in size and represented on a single
tile (Fig. 3). I give an example from Lucca Cathedral. It is on one of the porch
piers, and is 19½ inches in diameter. A writer in 1858 says that, "from the
continual attrition it has received from thousands of tracing fingers, a central
group of Theseus and the Minotaur has now been very nearly effaced." Other
examples were, and perhaps still are, to be found in the Abbey of Toussarts, at
Châlons-sur-Marne, in the very ancient church of St. Michele at Pavia, at Aix in
Provence, in the cathedrals of Poitiers, Rheims, and Arras, in the church of
Santa Maria in Aquiro in Rome, in San Vitale at Ravenna, in the Roman mosaic
pavement found at Salzburg, and elsewhere. These mazes were sometimes called
"Chemins de Jerusalem," as being emblematical of the difficulties attending a
journey to the earthly Jerusalem and of those encountered by the Christian
before he can reach the heavenly Jerusalem—where the centre was frequently
called "Ciel."
Common as these mazes were upon the Continent, it is probable that no example
is to be found in any English church; at least I am not aware of the existence
of any. But almost every county has, or has had, its specimens of mazes cut in the
turf. Though these are frequently known as "miz-mazes" or "mize-mazes," it is
not uncommon to find them locally called "Troy-towns," "shepherds' races," or
"Julian's Bowers"—names that are misleading, as suggesting a false origin. From
the facts alone that many of these English turf mazes are clearly copied from
those in the Continental churches, and practically all are found close to some
ecclesiastical building or near the site of an ancient one, we may regard it as
certain that they were of church origin and not invented by the shepherds or
other rustics. And curiously enough, these turf mazes are apparently unknown on
the Continent. They are distinctly mentioned by Shakespeare:—
"The nine men's morris is filled up with
mud,
And the quaint mazes in the wanton
green
For lack of tread are
undistinguishable."
A Midsummer Night's Dream, ii.
1.
"My old bones ache: here's a maze trod
indeed,
Through forth-rights and
meanders!"
The Tempest, iii.
3.
There was such a maze at Comberton, in Cambridgeshire, and another, locally
called the "miz-maze," at Leigh, in Dorset. The latter was on the highest part
of a field on the top of a hill, a quarter of a mile from the village, and was
slightly hollow in the middle and enclosed by a bank about 3 feet high. It was
circular, and was thirty paces in diameter. In 1868 the turf had grown over the
little trenches, and it was then impossible to trace the paths of the maze. The
Comberton one was at the same date believed to be perfect, but whether either or
both have now disappeared I cannot say. Nor have I been able to verify the
existence or non-existence of the other examples of which I am able to give
illustrations. I shall therefore write of them all in the past tense, retaining
the hope that some are still preserved.
 FIG. 4.—Maze at Saffron Walden, Essex. FIG. 4.—Maze at Saffron Walden, Essex.
In the next two mazes given—that at Saffron Walden, Essex (110 feet in
diameter, Fig. 4), and the one near St. Anne's Well, at Sneinton,
Nottinghamshire (Fig. 5), which was ploughed up on February 27th, 1797 (51 feet
in diameter, with a path 535 yards long)—the paths must in each case be
understood to be on the lines, black or white, as the case may be.
 FIG. 5.—Maze at Sneinton, Nottinghamshire. FIG. 5.—Maze at Sneinton, Nottinghamshire.
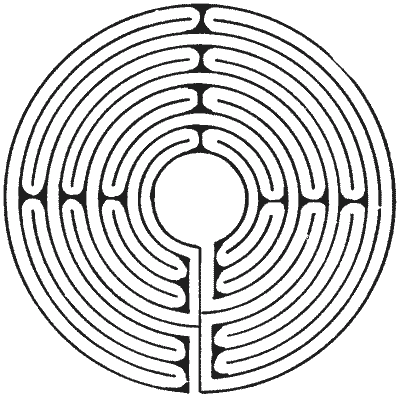 FIG. 6.—Maze at Alkborough, Lincolnshire. FIG. 6.—Maze at Alkborough, Lincolnshire.
I give in Fig. 6 a maze that was at Alkborough, Lincolnshire, overlooking the
Humber. This was 44 feet in diameter, and the resemblance between it and the mazes at Chartres
and Lucca (Figs. 2 and 3) will be at once perceived. A maze at Boughton Green,
in Nottinghamshire, a place celebrated at one time for its fair (Fig. 7), was 37
feet in diameter. I also include the plan (Fig. 8) of one that used to be on the
outskirts of the village of Wing, near Uppingham, Rutlandshire. This maze was 40
feet in diameter.
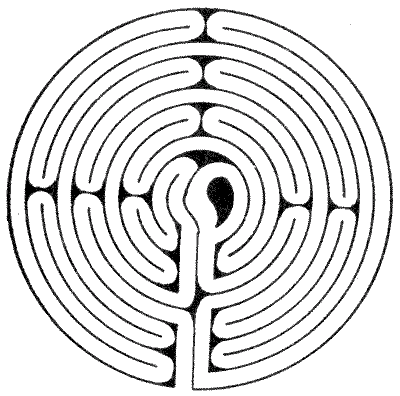 FIG. 7.—Maze at Boughton Green,
Nottinghamshire. FIG. 7.—Maze at Boughton Green,
Nottinghamshire.
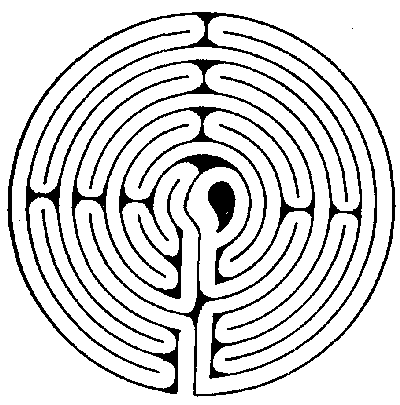 FIG. 8.—Maze at Wing, Rutlandshire. FIG. 8.—Maze at Wing, Rutlandshire.
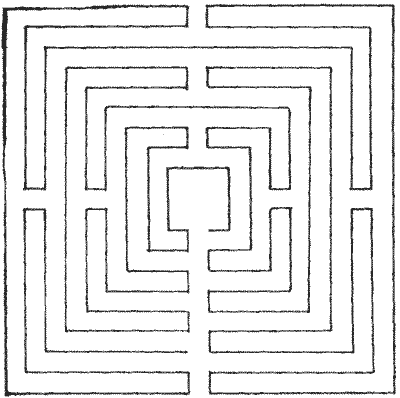 FIG. 9.—Maze on St. Catherine's Hill,
Winchester. FIG. 9.—Maze on St. Catherine's Hill,
Winchester.
The maze that was on St. Catherine's Hill, Winchester, in the parish of
Chilcombe, was a poor specimen (Fig. 9), since, as will be seen, there was one
short direct route to the centre, unless, as in Fig. 10 again, the path is the
line itself from end to end. This maze was 86 feet square, cut in the turf, and
was locally known as the "Mize-maze." It became very indistinct about 1858, and
was then recut by the Warden of Winchester, with the aid of a plan possessed by
a lady living in the neighbourhood.
 FIG. 10.—Maze on Ripon Common. FIG. 10.—Maze on Ripon Common.
A maze formerly existed on Ripon Common, in Yorkshire (Fig. 10). It was
ploughed up in 1827, but its plan was fortunately preserved. This example was 20
yards in diameter, and its path is said to have been 407 yards long.
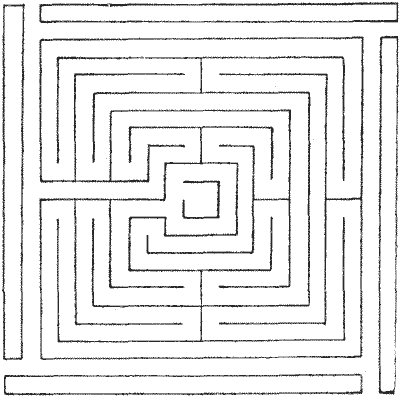 FIG. 11.—Maze at Theobalds, Hertfordshire. FIG. 11.—Maze at Theobalds, Hertfordshire.
In the case of the maze at Theobalds, Hertfordshire, after you have found the
entrance within the four enclosing hedges, the path is forced (Fig. 11). As further
illustrations of this class of maze, I give one taken from an Italian work on
architecture by Serlio, published in 1537 (Fig. 12), and one by London and Wise,
the designers of the Hampton Court maze, from their book, The Retired
Gard'ner, published in 1706 (Fig. 13). Also, I add a Dutch maze (Fig.
14).
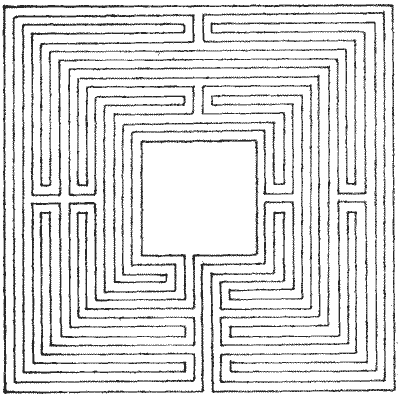 FIG. 12.—Italian Maze of Sixteenth
Century. FIG. 12.—Italian Maze of Sixteenth
Century.
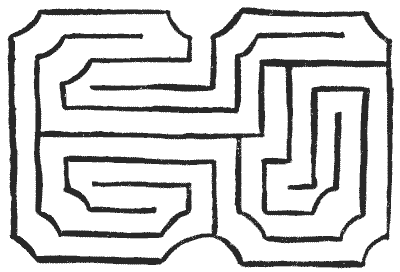 FIG. 13.—By the Designers of Hampton Court
Maze. FIG. 13.—By the Designers of Hampton Court
Maze.
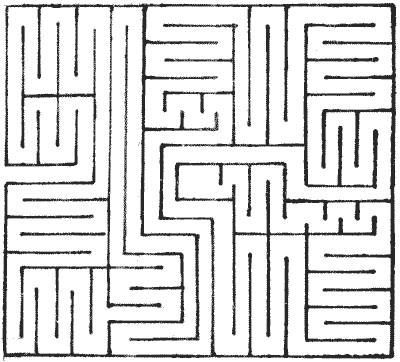 FIG. 14.—A Dutch Maze. FIG. 14.—A Dutch Maze.
So far our mazes have been of historical interest, but they have presented no
difficulty in threading. After the Reformation period we find mazes converted
into mediums for recreation, and they generally consisted of labyrinthine paths
enclosed by thick and carefully trimmed hedges. These topiary hedges were known
to the Romans, with whom the topiarius was the ornamental gardener. This
type of maze has of late years degenerated into the seaside "Puzzle Gardens.
Teas, sixpence, including admission to the Maze." The Hampton Court Maze,
sometimes called the "Wilderness," at the royal palace, was designed, as I have
said, by London and Wise for William III., who had a liking for such things
(Fig. 15). I have before me some three or four versions of it, all slightly
different from one another; but the plan I select is taken from an old
guide-book to the palace, and therefore ought to be trustworthy. The meaning of
the dotted lines, etc., will be explained later on.
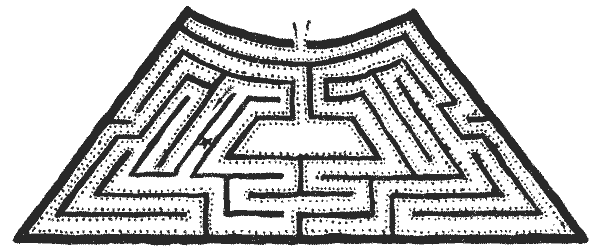 FIG. 15.—Maze at Hampton Court Palace. FIG. 15.—Maze at Hampton Court Palace.
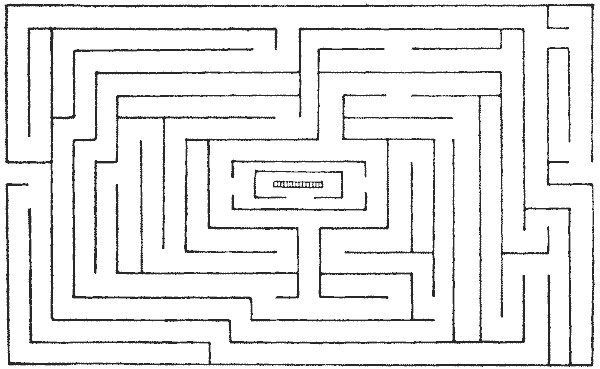 FIG. 16.—Maze at Hatfield House, Herts. FIG. 16.—Maze at Hatfield House, Herts.
The maze at Hatfield House (Fig. 16), the seat of the Marquis of Salisbury,
like so many labyrinths, is not difficult on paper; but both this and the Hampton
Court Maze may prove very puzzling to actually thread without knowing the plan.
One reason is that one is so apt to go down the same blind alleys over and over
again, if one proceeds without method. The maze planned by the desire of the
Prince Consort for the Royal Horticultural Society's Gardens at South Kensington
was allowed to go to ruin, and was then destroyed—no great loss, for it was a
feeble thing. It will be seen that there were three entrances from the outside
(Fig. 17), but the way to the centre is very easy to discover. I include a
German maze that is curious, but not difficult to thread on paper (Fig. 18). The
example of a labyrinth formerly existing at Pimperne, in Dorset, is in a class
by itself (Fig. 19). It was formed of small ridges about a foot high, and
covered nearly an acre of ground; but it was, unfortunately, ploughed up
in 1730.
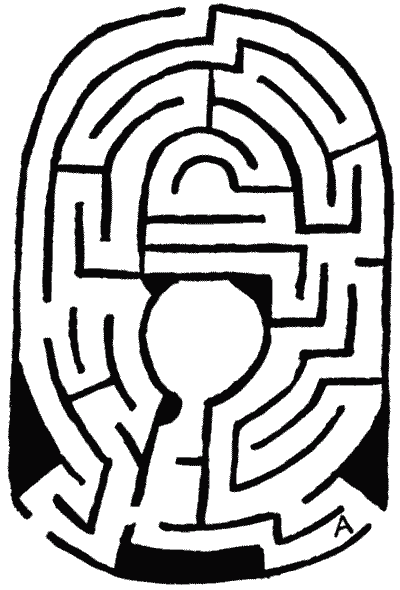 FIG. 17.—Maze formerly at South
Kensington. FIG. 17.—Maze formerly at South
Kensington.
 FIG. 18.—A German Maze. FIG. 18.—A German Maze.
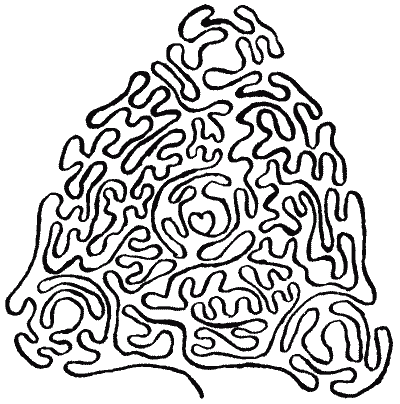 FIG. 19.—Maze at Pimperne, Dorset. FIG. 19.—Maze at Pimperne, Dorset.
We will now pass to the interesting subject of how to thread any maze. While
being necessarily brief, I will try to make the matter clear to readers who have
no knowledge of mathematics. And first of all we will assume that we are trying
to enter a maze (that is, get to the "centre") of which we have no plan and
about which we know nothing. The first rule is this: If a maze has no parts of
its hedges detached from the rest, then if we always keep in touch with the
hedge with the right hand (or always touch it with the left), going down to the
stop in every blind alley and coming back on the other side, we shall pass
through every part of the maze and make our exit where we went in. Therefore we
must at one time or another enter the centre, and every alley will be traversed
twice.
Now look at the Hampton Court plan. Follow, say to the right, the path
indicated by the dotted line, and what I have said is clearly correct if
we obliterate the two detached parts, or "islands," situated on each side of the
star. But as these islands are there, you cannot by this method traverse every
part of the maze; and if it had been so planned that the "centre" was, like the
star, between the two islands, you would never pass through the "centre" at all.
A glance at the Hatfield maze will show that there are three of these detached
hedges or islands at the centre, so this method will never take you to the
"centre" of that one. But the rule will at least always bring you safely out
again unless you blunder in the following way. Suppose, when you were going in
the direction of the arrow in the Hampton Court Maze, that you could not
distinctly see the turning at the bottom, that you imagined you were in a blind
alley and, to save time, crossed at once to the opposite hedge, then you would
go round and round that U-shaped island with your right hand still always on the
hedge—for ever after!
This blunder happened to me a few years ago in a little maze on the isle of
Caldy, South Wales. I knew the maze was a small one, but after a very long walk
I was amazed to find that I did not either reach the "centre" or get out again.
So I threw a piece of paper on the ground, and soon came round to it; from which
I knew that I had blundered over a supposed blind alley and was going round and
round an island. Crossing to the opposite hedge and using more care, I was
quickly at the centre and out again. Now, if I had made a similar mistake at
Hampton Court, and discovered the error when at the star, I should merely have
passed from one island to another! And if I had again discovered that I was on a
detached part, I might with ill luck have recrossed to the first island again!
We thus see that this "touching the hedge" method should always bring us safely
out of a maze that we have entered; it may happen to take us through the
"centre," and if we miss the centre we shall know there must be islands. But it
has to be done
with a little care, and in no case can we be sure that we have traversed every
alley or that there are no detached parts.
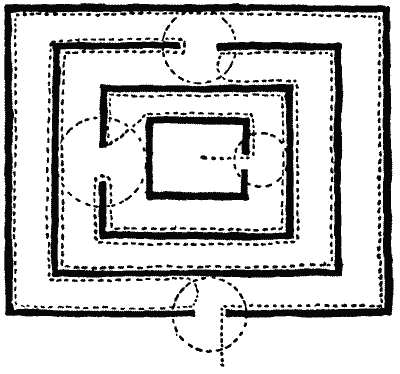 FIG. 20.—M. Tremaux's Method of Solution. FIG. 20.—M. Tremaux's Method of Solution.
If the maze has many islands, the traversing of the whole of it may be a
matter of considerable difficulty. Here is a method for solving any maze, due to
M. Trémaux, but it necessitates carefully marking in some way your entrances and
exits where the galleries fork. I give a diagram of an imaginary maze of a very
simple character that will serve our purpose just as well as something more
complex (Fig. 20). The circles at the regions where we have a choice of turnings
we may call nodes. A "new" path or node is one that has not been entered before
on the route; an "old" path or node is one that has already been entered, 1. No
path may be traversed more than twice. 2. When you come to a new node, take any
path you like. 3. When by a new path you come to an old node or to the stop of a
blind alley, return by the path you came. 4. When by an old path you come to an
old node, take a new path if there is one; if not, an old path. The route
indicated by the dotted line in the diagram is taken in accordance with these
simple rules, and it will be seen that it leads us to the centre, although the
maze consists of four islands.
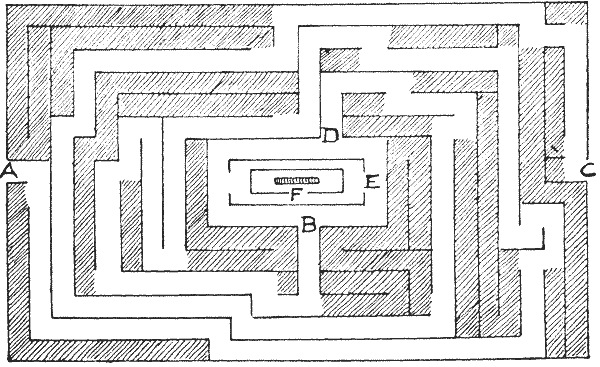 FIG. 21.—How to thread the Hatfield Maze. FIG. 21.—How to thread the Hatfield Maze.
Neither of
the methods I have given will disclose to us the shortest way to the centre, nor
the number of the different routes. But we can easily settle these points with a
plan. Let us take the Hatfield maze (Fig. 21). It will be seen that I have
suppressed all the blind alleys by the shading. I begin at the stop and work
backwards until the path forks. These shaded parts, therefore, can never be
entered without our having to retrace our steps. Then it is very clearly seen
that if we enter at A we must come out at B; if we enter at C we must come out
at D. Then we have merely to determine whether A, B, E, or C, D, E, is the
shorter route. As a matter of fact, it will be found by rough measurement or
calculation that the shortest route to the centre is by way of C, D, E, F.
I will now give three mazes that are simply puzzles on paper, for, so far as
I know, they have never been constructed in any other way. The first I will call
the Philadelphia maze (Fig. 22). Fourteen years ago a travelling salesman, living in
Philadelphia, U.S.A., developed a curiously unrestrained passion for puzzles. He
neglected his business, and soon his position was taken from him. His days and
nights were now passed with the subject that fascinated him, and this little
maze seems to have driven him into insanity. He had been puzzling over it for
some time, and finally it sent him mad and caused him to fire a bullet through
his brain. Goodness knows what his difficulties could have been! But there can
be little doubt that he had a disordered mind, and that if this little puzzle
had not caused him to lose his mental balance some other more or less trivial
thing would in time have done so. There is no moral in the story, unless it be
that of the Irish maxim, which applies to every occupation of life as much as to
the solving of puzzles: "Take things aisy; if you can't take them aisy, take
them as aisy as you can." And it is a bad and empirical way of solving any
puzzle—by blowing your brains out.
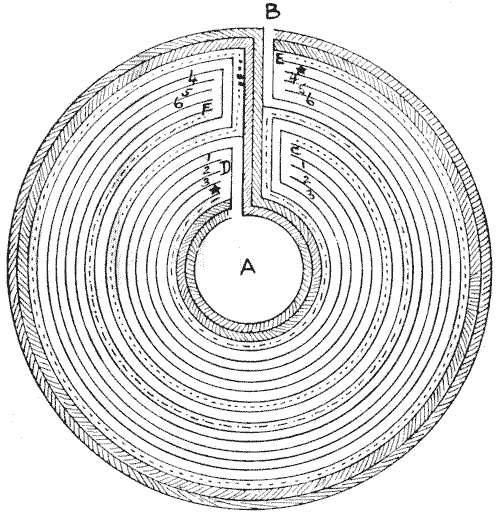 FIG. 22. The Philadelphia Maze, and its
Solution. FIG. 22. The Philadelphia Maze, and its
Solution.
Now, how many different routes are there from A to B in this maze if we must
never in any route go along the same passage twice? The four open spaces where
four passages end are not reckoned as "passages." In the diagram (Fig. 22) it
will be seen that I have again suppressed the blind alleys. It will be found
that, in any case, we must go from A to C, and also from F to B. But when we
have arrived at C there are three ways, marked 1, 2, 3, of getting to D.
Similarly, when we get to E there are three ways, marked 4, 5, 6, of getting to
F. We have also the dotted route from C to E, the other dotted route from D to
F, and the passage from D to E, indicated by stars. We can, therefore, express
the position of affairs by the little diagram annexed (Fig. 23). Here every
condition of route exactly corresponds to that in the circular maze, only it is
much less confusing to the eye. Now, the number of routes, under the conditions,
from A to B on this simplified diagram is 640, and that is the required answer
to the maze puzzle.
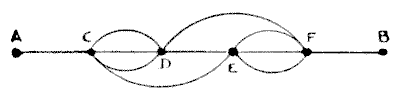 FIG. 23.—Simplified Diagram of Fig. 22. FIG. 23.—Simplified Diagram of Fig. 22.
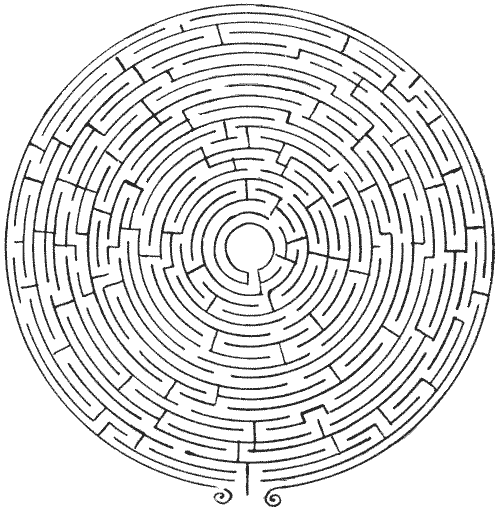 FIG. 24.—Can you find the Shortest Way to
Centre? FIG. 24.—Can you find the Shortest Way to
Centre?
Finally, I will leave two easy maze puzzles (Figs. 24, 25) for my readers to
solve for themselves. The puzzle in each case is to find the shortest possible
route to the centre. Everybody knows the story of Fair Rosamund and the
Woodstock maze. What the maze was like or whether it ever existed except in
imagination is not known, many writers believing that it was simply a
badly-constructed house with a large number of confusing rooms and passages. At
any rate, my sketch lacks the authority of the other mazes in this article. My
"Rosamund's Bower" is simply designed to show that where you have the plan
before you it often happens that the easiest way to find a route into a maze is
by working backwards and first finding a way out.
 FIG. 25.—Rosamund's Bower. FIG. 25.—Rosamund's Bower.
Previous Next
|