|
UNCLASSIFIED
PROBLEMS.
"A snapper up of unconsidered trifles."
Winter's Tale, iv. 2.
414.—WHO
WAS FIRST?
Anderson, Biggs, and Carpenter were staying together at a place by the
seaside. One day they went out in a boat and were a mile at sea when a rifle was
fired on shore in their direction. Why or by whom the shot was fired fortunately
does not concern us, as no information on these points is obtainable, but from
the facts I picked up we can get material for a curious little puzzle for the
novice.
It seems that Anderson only heard the report of the gun, Biggs only saw the
smoke, and Carpenter merely saw the bullet strike the water near them. Now, the
question arises: Which of them first knew of the discharge of the rifle?
Solution 415.—A
WONDERFUL VILLAGE.
There is a certain village in Japan, situated in a very low valley, and yet
the sun is nearer to the inhabitants every noon, by 3,000 miles and upwards,
than when he either rises or sets to these people. In what part of the country
is the village situated?
Solution 416.—A
CALENDAR PUZZLE.
If the end of the world should come on the first day of a new century, can
you say what are the chances that it will happen on a Sunday?
Solution 417.—THE
TIRING IRONS.
The illustration represents one of the most ancient of all mechanical
puzzles. Its origin is unknown. Cardan, the mathematician, wrote about it in
1550, and Wallis in 1693; while it is said still to be found in obscure English
villages (sometimes deposited in strange places, such as a church belfry), made
of iron, and appropriately called "tiring-irons," and to be used by the
Norwegians to-day as a lock for boxes and bags. In the toyshops it is sometimes
called the "Chinese rings," though there seems to be no authority for the
description, and it more frequently goes by the unsatisfactory name of "the
puzzling rings." The French call it "Baguenaudier."
The puzzle will be seen to consist of a simple loop of wire fixed in a
handle to be held in the left hand, and a certain number of rings secured
by wires which pass through holes in the bar and are kept there by
their blunted ends. The wires work freely in the bar, but cannot come apart from
it, nor can the wires be removed from the rings. The general puzzle is to detach
the loop completely from all the rings, and then to put them all on again.
Now, it will be seen at a glance that the first ring (to the right) can be
taken off at any time by sliding it over the end and dropping it through the
loop; or it may be put on by reversing the operation. With this exception, the
only ring that can ever be removed is the one that happens to be a contiguous
second on the loop at the right-hand end. Thus, with all the rings on, the
second can be dropped at once; with the first ring down, you cannot drop the
second, but may remove the third; with the first three rings down, you cannot
drop the fourth, but may remove the fifth; and so on. It will be found that the
first and second rings can be dropped together or put on together; but to
prevent confusion we will throughout disallow this exceptional double move, and
say that only one ring may be put on or removed at a time.
We can thus take off one ring in 1 move; two rings in 2 moves; three rings in
5 moves; four rings in 10 moves; five rings in 21 moves; and if we keep on
doubling (and adding one where the number of rings is odd) we may easily
ascertain the number of moves for completely removing any number of rings. To
get off all the seven rings requires 85 moves. Let us look at the five moves
made in removing the first three rings, the circles above the line standing for
rings on the loop and those under for rings off the loop.
Drop the first ring; drop the third; put up the first; drop the second; and
drop the first—5 moves, as shown clearly in the diagrams. The dark circles show
at each stage, from the starting position to the finish, which rings it is
possible to drop. After move 2 it will be noticed that no ring can be dropped
until one has been put on, because the first and second rings from the right now
on the loop are not together. After the fifth move, if we wish to remove all
seven rings we
must now drop the fifth. But before we can then remove the fourth it is
necessary to put on the first three and remove the first two. We shall then have
7, 6, 4, 3 on the loop, and may therefore drop the fourth. When we have put on 2
and 1 and removed 3, 2, 1, we may drop the seventh ring. The next operation then
will be to get 6, 5, 4, 3, 2, 1 on the loop and remove 4, 3, 2, 1, when 6 will
come off; then get 5, 4, 3, 2, 1 on the loop, and remove 3, 2, 1, when 5 will
come off; then get 4, 3, 2, 1 on the loop and remove 2, 1, when 4 will come off;
then get 3, 2, 1 on the loop and remove 1, when 3 will come off; then get 2, 1
on the loop, when 2 will come off; and 1 will fall through on the 85th move,
leaving the loop quite free. The reader should now be able to understand the
puzzle, whether or not he has it in his hand in a practical form.
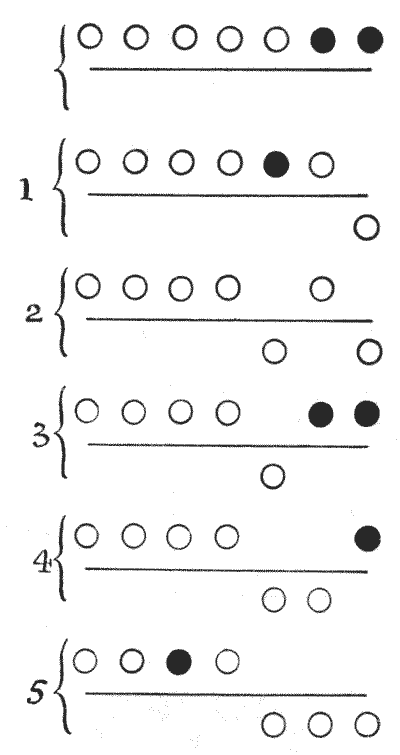
The particular problem I propose is simply this. Suppose there are altogether
fourteen rings on the tiring-irons, and we proceed to take them all off in the
correct way so as not to waste any moves. What will be the position of the rings
after the 9,999th move has been made?
Solution 418.—SUCH
A GETTING UPSTAIRS.
In a suburban villa there is a small staircase with eight steps, not counting
the landing. The little puzzle with which Tommy Smart perplexed his family is
this. You are required to start from the bottom and land twice on the floor
above (stopping there at the finish), having returned once to the ground floor.
But you must be careful to use every tread the same number of times. In how few
steps can you make the ascent? It seems a very simple matter, but it is more
than likely that at your first attempt you will make a great many more steps
than are necessary. Of course you must not go more than one riser at a time.
Tommy knows the trick, and has shown it to his father, who professes to have
a contempt for such things; but when the children are in bed the pater will
often take friends out into the hall and enjoy a good laugh at their
bewilderment. And yet it is all so very simple when you know how it is done.
Solution 419.—THE
FIVE PENNIES.
Here is a really hard puzzle, and yet its conditions are so absurdly simple.
Every reader knows how to place four pennies so that they are equidistant from
each other. All you have to do is to arrange three of them flat on the table so
that they touch one another in the form of a triangle, and lay the fourth penny
on top in the centre. Then, as every penny touches every other penny, they are
all at equal distances from one another. Now try to do the same thing with five
pennies—place them so that every penny shall touch every other penny—and you
will find it a different matter altogether.
Solution 420.—THE
INDUSTRIOUS BOOKWORM.
Our friend Professor Rackbrane is seen in the illustration to be propounding
another of his little posers. He is explaining that since he last had
occasion to take down those three volumes of a learned book from their place on
his shelves a bookworm has actually bored a hole straight through from the first
page to the last. He says that the leaves are together three inches thick in
each volume, and that every cover is exactly one-eighth of an inch thick, and he
asks how long a tunnel had the industrious worm to bore in preparing his new
tube railway. Can you tell him?
Solution 421.—A
CHAIN PUZZLE.
This is a puzzle based on a pretty little idea first dealt with by the late
Mr. Sam Loyd. A man had nine pieces of chain, as shown in the illustration. He
wanted to join these fifty links into one endless chain. It will cost a penny to
open any link and twopence to weld a link together again, but he could buy a new
endless chain of the same character and quality for 2s. 2d. What
was the cheapest course for him to adopt? Unless the reader is cunning he may
find himself a good way out in his answer.
Solution 422.—THE
SABBATH PUZZLE.
I have come across the following little poser in an old book. I wonder how
many readers will see the author's intended solution to the riddle.
Christians the week's first day for
Sabbath hold;
The Jews the
seventh, as they did of old;
The
Turks the sixth, as we have oft been told.
How can these three, in the same place and
day,
Have each his own true Sabbath?
tell, I pray.
Solution 423.—THE
RUBY BROOCH.
The annals of Scotland Yard contain some remarkable cases of jewel robberies,
but one of the most perplexing was the theft of Lady Littlewood's rubies. There
have, of course, been many greater robberies in point of value, but few so
artfully conceived. Lady Littlewood, of Romley Manor, had a beautiful but rather
eccentric heirloom in the form of a ruby brooch. While staying at her town house
early in the eighties she took the jewel to a shop in Brompton for some slight
repairs.
"A fine collection of rubies, madam," said the shopkeeper, to whom her
ladyship was a stranger.
"Yes," she replied; "but curiously enough I have never actually counted them.
My mother once pointed out to me that if you start from the centre and count up
one line, along the outside and down the next line, there are always eight
rubies. So I should always know if a stone were missing."
Six months later a brother of Lady Littlewood's, who had returned from his regiment
in India, noticed that his sister was wearing the ruby brooch one night at a
county ball, and on their return home asked to look at it more closely. He
immediately detected the fact that four of the stones were gone.
"How can that possibly be?" said Lady Littlewood. "If you count up one line
from the centre, along the edge, and down the next line, in any direction, there
are always eight stones. This was always so and is so now. How, therefore, would
it be possible to remove a stone without my detecting it?"
"Nothing could be simpler," replied the brother. "I know the brooch well. It
originally contained forty-five stones, and there are now only forty-one.
Somebody has stolen four rubies, and then reset as small a number of the others
as possible in such a way that there shall always be eight in any of the
directions you have mentioned."
There was not the slightest doubt that the Brompton jeweller was the thief,
and the matter was placed in the hands of the police. But the man was wanted for
other robberies, and had left the neighbourhood some time before. To this day he
has never been found.
The interesting little point that at first baffled the police, and which
forms the subject of our puzzle, is this: How were the forty-five rubies
originally arranged on the brooch? The illustration shows exactly how the
forty-one were arranged after it came back from the jeweller; but although they
count eight correctly in any of the directions mentioned, there are four stones
missing.
Solution 424.—THE
DOVETAILED BLOCK.
Here is a curious mechanical puzzle that was given to me some years ago, but
I cannot say who first invented it. It consists of two solid blocks of wood
securely dovetailed together. On the other two vertical sides that are not
visible the appearance is precisely the same as on those shown. How were the
pieces put together? When I published this little puzzle in a London newspaper I
received (though they were unsolicited) quite a stack of models, in oak, in
teak, in mahogany, rosewood, satinwood, elm, and deal; some half a foot in
length, and others varying in size right down to a delicate little model about
half an inch square. It seemed to create considerable interest.
Solution 425.—JACK
AND THE BEANSTALK.
The illustration, by a British artist, is a sketch of Jack climbing the
beanstalk. Now, the artist has made a serious blunder in this drawing. Can you
find out what it is?
Solution 426.—THE
HYMN-BOARD POSER.
The worthy vicar of Chumpley St. Winifred is in great distress. A little
church difficulty has arisen that all the combined intelligence of the parish
seems unable to surmount. What this difficulty is I will state hereafter, but it
may add to the interest of the problem if I first give a short account of the
curious position that has been brought about. It all has to do with the church
hymn-boards, the plates of which have become so damaged that they have ceased to
fulfil the purpose for which they were devised. A generous parishioner has
promised to pay for a new set of plates at a certain rate of cost; but strange
as it may seem, no agreement can be come to as to what that cost should be. The
proposed maker of the plates has named a price which the donor declares to be absurd. The good
vicar thinks they are both wrong, so he asks the schoolmaster to work out the
little sum. But this individual declares that he can find no rule bearing on the
subject in any of his arithmetic books. An application having been made to the
local medical practitioner, as a man of more than average intellect at Chumpley,
he has assured the vicar that his practice is so heavy that he has not had time
even to look at it, though his assistant whispers that the doctor has been
sitting up unusually late for several nights past. Widow Wilson has a smart son,
who is reputed to have once won a prize for puzzle-solving. He asserts that as
he cannot find any solution to the problem it must have something to do with the
squaring of the circle, the duplication of the cube, or the trisection of an
angle; at any rate, he has never before seen a puzzle on the principle, and he
gives it up.
This was the state of affairs when the assistant curate (who, I should say,
had frankly confessed from the first that a profound study of theology had
knocked out of his head all the knowledge of mathematics he ever possessed)
kindly sent me the puzzle.
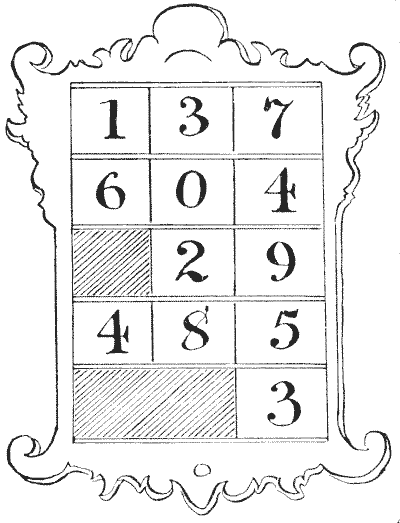
A church has three hymn-boards, each to indicate the numbers of five
different hymns to be sung at a service. All the boards are in use at the same
service. The hymn-book contains 700 hymns. A new set of numbers is required, and
a kind parishioner offers to present a set painted on metal plates, but
stipulates that only the smallest number of plates necessary shall be purchased.
The cost of each plate is to be 6d., and for the painting of each plate
the charges are to be: For one plate, 1s.; for two plates alike,
11¾d. each; for three plates alike, 11½d. each, and so on, the
charge being one farthing less per plate for each similarly painted plate. Now,
what should be the lowest cost?
Readers will note that they are required to use every legitimate and
practical method of economy. The illustration will make clear the nature of the
three hymn-boards and plates. The five hymns are here indicated by means of
twelve plates. These plates slide in separately at the back, and in the
illustration there is room, of course, for three more plates.
Solution 427.—PHEASANT-SHOOTING.
A Cockney friend, who is very apt to draw the long bow, and is evidently less
of a sportsman than he pretends to be, relates to me the following not very
credible yarn:—
"I've just been pheasant-shooting with my friend the duke. We had splendid
sport, and I made some wonderful shots. What do you think of this, for instance?
Perhaps you can twist it into a puzzle. The duke and I were crossing a field
when suddenly twenty-four pheasants rose on the wing right in front of us. I
fired, and two-thirds of them dropped dead at my feet. Then the duke had a shot
at what were left, and brought down three-twenty-fourths of them, wounded in the
wing. Now, out of those twenty-four birds, how many still remained?"
It seems a simple enough question, but can the reader give a correct
answer?
Solution 428.—THE
GARDENER AND THE COOK.
A correspondent, signing himself "Simple Simon," suggested that I should give
a special catch puzzle in the issue of The Weekly Dispatch for All Fools'
Day, 1900. So I gave the following, and it caused considerable amusement; for
out of a very large body of competitors, many quite expert, not a single person
solved it, though it ran for nearly a month.
"The illustration is a fancy sketch of my correspondent, 'Simple Simon,' in
the act of trying to solve the following innocent little arithmetical puzzle. A race between a
man and a woman that I happened to witness one All Fools' Day has fixed itself
indelibly on my memory. It happened at a country-house, where the gardener and
the cook decided to run a race to a point 100 feet straight away and return. I
found that the gardener ran 3 feet at every bound and the cook only 2 feet, but
then she made three bounds to his two. Now, what was the result of the
race?"
A fortnight after publication I added the following note: "It has been
suggested that perhaps there is a catch in the 'return,' but there is not. The
race is to a point 100 feet away and home again—that is, a distance of 200 feet.
One correspondent asks whether they take exactly the same time in turning, to
which I reply that they do. Another seems to suspect that it is really a
conundrum, and that the answer is that 'the result of the race was a
(matrimonial) tie.' But I had no such intention. The puzzle is an arithmetical
one, as it purports to be."
Solution 429.—PLACING
HALFPENNIES.
Here is an interesting little puzzle suggested to me by Mr. W. T. Whyte. Mark
off on a sheet of paper a rectangular space 5 inches by 3 inches, and then find
the greatest number of halfpennies that can be placed within the enclosure under
the following conditions. A halfpenny is exactly an inch in diameter. Place your
first halfpenny where you like, then place your second coin at exactly the
distance of an inch from the first, the third an inch distance from the second,
and so on. No halfpenny may touch another halfpenny or cross the boundary. Our
illustration will make the matter perfectly clear. No. 2 coin is an inch from
No. 1; No. 3 an inch from No. 2; No. 4 an inch from No. 3; but after No. 10 is
placed we can go no further in this attempt. Yet several more halfpennies might
have been got in. How many can the reader place?
Solution 430.—FIND
THE MAN'S WIFE.
One summer day in 1903 I was loitering on the Brighton front, watching the
people strolling about on the beach, when the friend who was with me suddenly
drew my attention to an individual who was standing alone, and said, "Can you
point out that man's wife? They are stopping at the same hotel as I am, and the
lady is one of those in view." After a few minutes' observation, I was
successful in indicating the lady correctly. My friend was curious to know by
what method of reasoning I had arrived at the result. This was my answer:—
"We may at once exclude that Sister of Mercy and the girl in the short frock;
also the woman selling oranges. It cannot be the lady in widows' weeds. It is
not the lady in the bath chair, because she is not staying at your hotel, for I
happened to see her come out of a private house this morning assisted by her
maid. The two ladies in red breakfasted at my hotel this morning, and as they
were not wearing outdoor dress I conclude they are staying there. It therefore
rests between the lady in blue and the one with the green parasol. But the left
hand that holds the parasol is, you see, ungloved and bears no wedding-ring.
Consequently I am driven to the conclusion that the lady in blue is the man's
wife—and you say this is correct."
Now, as my friend was an artist, and as I thought an amusing puzzle might be
devised on the lines of his question, I asked him to make me a drawing according
to some directions that I gave him, and I have pleasure in presenting his
production to my readers. It will be seen that the picture shows six men and six
ladies: Nos. 1, 3, 5, 7, 9, and 11 are ladies, and Nos. 2, 4, 6, 8, 10, and 12
are men. These twelve individuals represent six married couples, all strangers
to one another, who, in walking aimlessly about, have got mixed up. But we are
only concerned with the man that is wearing a straw hat—Number 10. The puzzle is
to find this man's wife. Examine the six ladies carefully, and see if you can
determine which one of them it is.
I showed the picture at the time to a few friends, and they expressed very
different opinions on the matter. One said, "I don't believe he would marry a
girl like Number 7." Another said, "I am sure a nice girl like Number 3 would
not marry such a fellow!" Another said, "It must be Number 1, because she has
got as far away as possible from the brute!" It was suggested, again, that it
must be Number 11, because "he seems to be looking towards her;" but a cynic
retorted, "For that very reason, if he is really looking at her, I should say
that she is not his wife!"
I now leave the question in the hands of my readers. Which is really Number
10's wife?
The illustration is of necessity considerably reduced from the large scale on
which it originally appeared in The Weekly Dispatch (24th May 1903), but
it is hoped that the details will be sufficiently clear to allow the reader to
derive entertainment from its examination. In any case the solution given will
enable him to follow the points with interest.
Solution
Previous
This was the last Puzzle
|