|
COMBINATION
AND GROUP PROBLEMS.
"A combination and a form indeed."
Hamlet, iii. 4.
Various puzzles in this class might be termed problems in the "geometry of
situation," but their solution really depends on the theory of combinations
which, in its turn, is derived directly from the theory of permutations. It has
seemed convenient to include here certain group puzzles and enumerations that
might, perhaps, with equal reason have been placed elsewhere; but readers are
again asked not to be too critical about the classification, which is very
difficult and arbitrary. As I have included my problem of "The Round Table" (No.
273), perhaps a few remarks on another well-known problem of the same class,
known by the French as La Problême des Ménages, may be interesting. If n
married ladies are seated at a round table in any determined order, in how many
different ways may their n husbands be placed so that every man is
between two ladies but never next to his own wife?
This difficult problem was first solved by Laisant, and the method shown in
the following table is due to Moreau:—
| 4 |
0 |
2 |
| 5 |
3 |
13 |
| 6 |
13 |
80 |
| 7 |
83 |
579 |
| 8 |
592 |
4738 |
| 9 |
4821 |
43387 |
| 10 |
43979 |
439792 |
The first column shows the number of married couples. The numbers in the
second column are obtained in this way:
5 × 3 + 0 - 2 = 13; 6 × 13 +
3 + 2 = 83;
7 × 83 + 13 - 2 = 592;
8 × 592 + 83 + 2 = 4821; and so on. Find
all the numbers, except 2, in the table, and the method will be evident. It will
be noted that the 2 is subtracted when the first number (the number of couples)
is odd, and added when that number is even. The numbers in the third column are
obtained thus: 13 - 0 = 13; 83 - 3 = 80;
592 - 13 = 579; 4821 - 83 = 4738; and so
on. The numbers in this last column give the required solutions. Thus, four
husbands may be seated in two ways, five husbands may be placed in thirteen
ways, and six husbands in eighty ways.
The following method, by Lucas, will show the remarkable way in which
chessboard analysis may be applied to the solution of a circular problem of this
kind. Divide a square into thirty-six cells, six by six, and strike out all the
cells in the long diagonal from the bottom left-hand corner to the top
right-hand corner, also the five cells in the diagonal next above it and the
cell in the bottom right-hand corner. The answer for six couples will be the
same as the number of ways in which you can place six rooks (not using the
cancelled cells) so that no rook shall ever attack another rook. It will be
found that the six rooks may be placed in eighty different ways, which agrees
with the above table.
262.—THOSE
FIFTEEN SHEEP.
A certain cyclopædia has the following curious problem, I am told: "Place
fifteen sheep in four pens so that there shall be the same number of sheep in
each pen." No answer whatever is vouchsafed, so I thought I would investigate
the matter. I saw that in dealing with apples or bricks the thing would appear
to be quite impossible, since four times any number must be an even number,
while fifteen is an odd number. I thought, therefore, that there must be some
quality peculiar to the sheep that was not generally known. So I decided to
interview some farmers on the subject. The first one pointed out that if we put
one pen inside another, like the rings of a target, and placed all sheep in the
smallest pen, it would be all right. But I objected to this, because you
admittedly place all the sheep in one pen, not in four pens. The second man said
that if I placed four sheep in each of three pens and three sheep in the last
pen (that is fifteen sheep in all), and one of the ewes in the last pen had a
lamb during the night, there would be the same number in each pen in the
morning. This also failed to satisfy me.

The third farmer said, "I've got four hurdle pens down in one of my fields,
and a small flock of wethers, so if you will just step down with me I will show
you how it is done." The illustration depicts my friend as he is about to
demonstrate the matter to me. His lucid explanation was evidently that which was
in the mind of the writer of the article in the cyclopædia. What was it? Can you
place those fifteen sheep?
Solution 263.—KING
ARTHUR'S KNIGHTS.
King Arthur sat at the Round Table on three successive evenings with his
knights—Beleobus, Caradoc, Driam, Eric, Floll, and Galahad—but on no occasion
did any person have as his neighbour one who had before sat next to him. On the
first evening they sat in alphabetical order round the table. But afterwards
King Arthur arranged the two next sittings so that he might have Beleobus as
near to him as possible and Galahad as far away from him as could be managed.
How did he seat the knights to the best advantage, remembering that rule that no
knight may have the same neighbour twice?
Solution 264.—THE
CITY LUNCHEONS.
Twelve men connected with a large firm in the City of London sit down to
luncheon together every day in the same room. The tables are small ones that
only accommodate two persons at the same time. Can you show how these twelve men
may lunch together on eleven days in pairs, so that no two of them shall ever
sit twice together? We will represent the men by the first twelve letters of the
alphabet, and suppose the first day's pairing to be as follows—
(A B) (C D) (E F) (G H) (I J) (K
L).
Then give any pairing you like for the next day, say—
(A C) (B D) (E G) (F H) (I K) (J
L),
and so on, until you have completed your eleven lines, with no pair ever
occurring twice. There are a good many different arrangements possible. Try to
find one of them.
Solution 265.—A
PUZZLE FOR CARD-PLAYERS.
Twelve members of a club arranged to play bridge together on eleven evenings,
but no player was ever to have the same partner more than once, or the same
opponent more than twice. Can you draw up a scheme showing how they may all sit
down at three tables every evening? Call the twelve players by the first twelve
letters of the alphabet and try to group them.
Solution 266.—A
TENNIS TOURNAMENT.
Four married couples played a "mixed double" tennis tournament, a man and a
lady always playing against a man and a lady. But no person ever played with or
against any other person more than once. Can you show how they all could have
played together in the two courts on three successive days? This is a little
puzzle of a quite practical kind, and it is just perplexing enough to be
interesting.
Solution 267.—THE
WRONG HATS.
"One of the most perplexing things I have come across lately," said Mr.
Wilson, "is this. Eight men had been dining not wisely but too well at a certain
London restaurant. They were the last to leave, but not one man was in a
condition to identify his own hat. Now, considering that they took their hats at
random, what are the chances that every man took a hat that did not belong to
him?"
"The first thing," said Mr. Waterson, "is to see in how many different ways
the eight hats could be taken."
"That is quite easy," Mr. Stubbs explained. "Multiply together the numbers,
1, 2, 3, 4, 5, 6, 7, and 8. Let me see—half a minute—yes; there are 40,320
different ways."
"Now all you've got to do is to see in how many of these cases no man has his
own hat," said Mr. Waterson.
"Thank you, I'm not taking any," said Mr. Packhurst. "I don't envy the man
who attempts the task of writing out all those forty-thousand-odd cases and then
picking out the ones he wants."
They all agreed that life is not long enough for that sort of amusement; and
as nobody saw any other way of getting at the answer, the matter was postponed
indefinitely. Can you solve the puzzle?
Solution 268.—THE
PEAL OF BELLS.
A correspondent, who is apparently much interested in campanology, asks me
how he is to construct what he calls a "true and correct" peal for four bells.
He says that every possible permutation of the four bells must be rung once, and
once only. He adds that no bell must move more than one place at a time, that no
bell must make more than two successive strokes in either the first or the last
place, and that the last change must be able to pass into the first. These
fantastic conditions will be found to be observed in the little peal for three
bells, as follows:—
| 1 |
2 |
3 |
| 2 |
1 |
3 |
| 2 |
3 |
1 |
| 3 |
2 |
1 |
| 3 |
1 |
2 |
| 1 |
3 |
2 |
How are we to give him a correct solution for his four bells?
Solution 269.—THREE
MEN IN A BOAT.
A certain generous London manufacturer gives his workmen every year a week's
holiday at the seaside at his own expense. One year fifteen of his men paid a
visit to Herne Bay. On the morning of their departure from London they were
addressed by their employer, who expressed the hope that they would have a very
pleasant time.
"I have been given to understand," he added, "that some of you fellows are
very fond of rowing, so I propose on this occasion to provide you with this
recreation, and at the same time give you an amusing little puzzle to solve.
During the seven days that you are at Herne Bay every one of you will go out
every day at the same time for a row, but there must always be three men in a
boat and no more. No two men may ever go out in a boat together more than once,
and no man is allowed to go out twice in the same boat. If you can manage to do
this, and use as few different boats as possible, you may charge the firm with
the expense."
One of the men tells me that the experience he has gained in such matters
soon enabled him to work out the answer to the entire satisfaction of themselves
and their employer. But the amusing part of the thing is that they never really
solved the little mystery. I find their method to have been quite incorrect, and
I think it will amuse my readers to discover how the men should have been placed
in the boats. As their names happen to have been Andrews, Baker, Carter, Danby,
Edwards, Frith, Gay, Hart, Isaacs, Jackson, Kent, Lang, Mason, Napper, and
Onslow, we can call them by their initials and write out the five groups for
each of the seven days in the following simple way:
|
1 |
2 |
3 |
4 |
5 |
| First Day: |
(ABC) |
(DEF) |
(GHI) |
(JKL) |
(MNO). |
The men within each pair of brackets are here seen to be in the same boat,
and therefore A can never go out with B or with C again, and C can never go out
again with B. The same applies to the other four boats. The figures show the
number on the boat, so that A, B, or C, for example, can never go out in boat
No. 1 again.
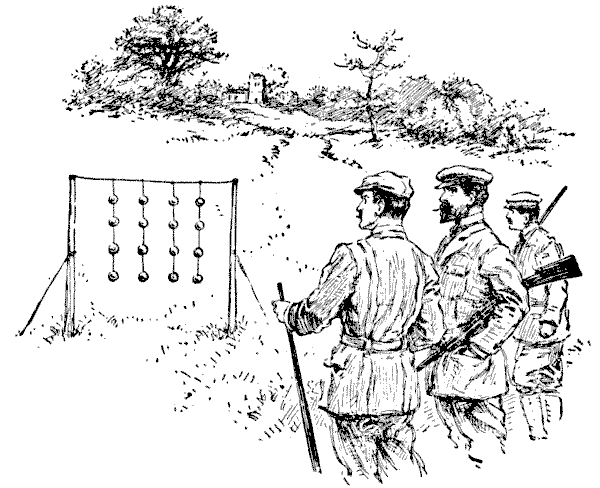
Solution 270.—THE
GLASS BALLS.
A number of clever marksmen were staying at a country house, and the host, to
provide a little amusement, suspended strings of glass balls, as shown in the
illustration, to be fired at. After they had all put their skill to a sufficient
test, somebody asked the following question: "What is the total number of
different ways in which these sixteen balls may be broken, if we must always
break the lowest ball that remains on any string?" Thus, one way would be to
break all the four balls on each string in succession, taking the strings from
left to right. Another would be to break all the fourth balls on the four
strings first, then break the three remaining on the first string, then take the
balls on the three other strings alternately from right to left, and so on.
There is such a vast number of different ways (since every little variation of
order makes a different way) that one is apt to be at first impressed by the
great difficulty of the problem. Yet it is really quite simple when once you
have hit on the proper method of attacking it. How many different ways are
there?
Solution 271.—FIFTEEN
LETTER PUZZLE.
| ALE |
FOE |
HOD |
BGN |
| CAB |
HEN |
JOG |
KFM |
| HAG |
GEM |
MOB |
BFH |
| FAN |
KIN |
JEK |
DFL |
| JAM |
HIM |
GCL |
LJH |
| AID |
JIB |
FCJ |
NJD |
| OAK |
FIG |
HCK |
MLN |
| BED |
OIL |
MCD |
BLK |
| ICE |
CON |
DGK |
The above is the solution of a puzzle I gave in Tit-bits in the summer
of 1896. It was required to take the letters, A, B, C, D, E, F, G, H, I, J, K,
L, M, N, and O, and with them form thirty-five groups of three letters so that
the combinations should include the greatest number possible of common English
words. No two letters may appear together in a group more than once. Thus, A and
L having been together in ALE, must never be found together again; nor may A
appear again in a group with E, nor L with E. These conditions will be found
complied with in the above solution, and the number of words formed is
twenty-one. Many persons have since tried hard to beat this number, but so far
have not succeeded.
More than thirty-five combinations of the fifteen letters cannot be formed
within the conditions. Theoretically, there cannot possibly be more than
twenty-three words formed, because only this number of combinations is possible
with a vowel or vowels in each. And as no English word can be formed from three
of the given vowels (A, E, I, and O), we must reduce the number of possible
words to twenty-two. This is correct theoretically, but practically that
twenty-second word cannot be got in. If JEK, shown above, were a word it would
be all right; but it is not, and no amount of juggling with the other letters
has resulted in a better answer than the one shown. I should, say that proper
nouns and abbreviations, such as Joe, Jim, Alf, Hal, Flo, Ike, etc., are
disallowed.
Now, the present puzzle is a variation of the above. It is simply this:
Instead of using the fifteen letters given, the reader is allowed to select any
fifteen different letters of the alphabet that he may prefer. Then construct
thirty-five groups in accordance with the conditions, and show as
many good English words as possible.
Solution 272.—THE
NINE SCHOOLBOYS.
This is a new and interesting companion puzzle to the "Fifteen Schoolgirls"
(see solution of No. 269), and even in the simplest possible form in which I
present it there are unquestionable difficulties. Nine schoolboys walk out in
triplets on the six week days so that no boy ever walks side by side with
any other boy more than once. How would you arrange them?
If we represent them by the first nine letters of the alphabet, they might be
grouped on the first day as follows:—
Then A can never walk again side by side with B, or B with C, or D with E,
and so on. But A can, of course, walk side by side with C. It is here not a
question of being together in the same triplet, but of walking side by side in a
triplet. Under these conditions they can walk out on six days; under the
"Schoolgirls" conditions they can only walk on four days.
Solution 273.—THE
ROUND TABLE.
Seat the same n persons at a round table on
occasions so that no person shall ever have the same two neighbours twice.
This is, of course, equivalent to saying that every person must sit once, and
once only, between every possible pair.
Solution 274.—THE
MOUSE-TRAP PUZZLE.
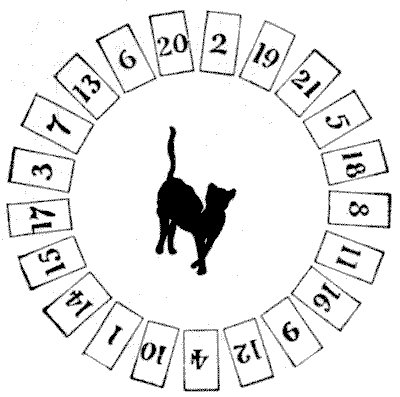
This is a modern version, with a difference, of an old puzzle of the same
name. Number twenty-one cards, 1, 2, 3, etc., up to 21, and place them in a
circle in the particular order shown in the illustration. These cards represent
mice. You start from any card, calling that card "one," and count, "one, two,
three," etc., in a clockwise direction, and when your count agrees with the
number on the card, you have made a "catch," and you remove the card. Then start
at the next card, calling that "one," and try again to make another "catch." And
so on. Supposing you start at 18, calling that card "one," your first "catch"
will be 19. Remove 19 and your next "catch" is 10. Remove 10 and your next
"catch" is 1. Remove the 1, and if you count up to 21 (you must never go
beyond), you cannot make another "catch." Now, the ideal is to "catch" all the
twenty-one mice, but this is not here possible, and if it were it would merely
require twenty-one different trials, at the most, to succeed. But the reader may
make any two cards change places before he begins. Thus, you can change the 6
with the 2, or the 7 with the 11, or any other pair. This can be done in several
ways so as to enable you to "catch" all the twenty-one mice, if you then start
at the right place. You may never pass over a "catch"; you must always remove
the card and start afresh.
Solution 275.—THE
SIXTEEN SHEEP.
Here is a new puzzle with matches and counters or coins. In the illustration
the matches represent hurdles and the counters sheep. The sixteen hurdles on the
outside, and the sheep, must be regarded as immovable; the puzzle has to do
entirely with the nine hurdles on the inside. It will be seen that at present
these nine hurdles enclose four groups of 8, 3, 3, and 2 sheep. The farmer
requires to readjust some of the hurdles so as to enclose 6, 6, and 4 sheep. Can
you do it by only replacing two hurdles? When you have succeeded, then try to do
it by replacing three hurdles; then four, five, six, and seven in succession. Of
course, the hurdles must be legitimately laid on the dotted lines, and no such
tricks are allowed as leaving unconnected ends of hurdles, or two hurdles placed
side by side, or merely making hurdles change places. In fact, the conditions
are so simple that any farm labourer will understand it directly.
Solution 276.—THE
EIGHT VILLAS.
In one of the outlying suburbs of London a man had a square plot of ground on
which he decided
to build eight villas, as shown in the illustration, with a common recreation
ground in the middle. After the houses were completed, and all or some of them
let, he discovered that the number of occupants in the three houses forming a
side of the square was in every case nine. He did not state how the occupants
were distributed, but I have shown by the numbers on the sides of the houses one
way in which it might have happened. The puzzle is to discover the total number
of ways in which all or any of the houses might be occupied, so that there
should be nine persons on each side. In order that there may be no
misunderstanding, I will explain that although B is what we call a reflection of
A, these would count as two different arrangements, while C, if it is turned
round, will give four arrangements; and if turned round in front of a mirror,
four other arrangements. All eight must be counted.

Solution 277.—COUNTER
CROSSES.
All that we need for this puzzle is nine counters, numbered 1, 2, 3, 4, 5, 6,
7, 8, and 9. It will be seen that in the illustration A these are arranged so as
to form a Greek cross, while in the case of B they form a Latin cross. In both
cases the reader will find that the sum of the numbers in the upright of the
cross is the same as the sum of the numbers in the horizontal arm. It is quite
easy to hit on such an arrangement by trial, but the problem is to discover in
exactly how many different ways it may be done in each case. Remember that
reversals and reflections do not count as different. That is to say, if you turn
this page round you get four arrangements of the Greek cross, and if you turn it
round again in front of a mirror you will get four more. But these eight are all
regarded as one and the same. Now, how many different ways are there in each
case?
Solution 278.—A
DORMITORY PUZZLE.
In a certain convent there were eight large dormitories on one floor,
approached by a spiral staircase in the centre, as shown in our plan. On an
inspection one Monday by the abbess it was found that the south aspect was so
much preferred that six times as many nuns slept on the south side as on each of
the other three sides. She objected to this overcrowding, and ordered that it
should be reduced. On Tuesday she found that five times as many slept on the
south side as on each of the other sides. Again she complained. On Wednesday she
found four times as many on the south side, on Thursday three times as many, and
on Friday twice as many. Urging the nuns to further efforts, she was pleased to
find on Saturday that an equal number slept on each of the four sides of the house.
What is the smallest number of nuns there could have been, and how might they
have arranged themselves on each of the six nights? No room may ever be
unoccupied.
Solution 279.—THE
BARRELS OF BALSAM.
A merchant of Bagdad had ten barrels of precious balsam for sale. They were
numbered, and were arranged in two rows, one on top of the other, as shown in
the picture. The smaller the number on the barrel, the greater was its value. So
that the best quality was numbered "1" and the worst numbered "10," and all the
other numbers of graduating values. Now, the rule of Ahmed Assan, the merchant,
was that he never put a barrel either beneath or to the right of one of less
value. The arrangement shown is, of course, the simplest way of complying with
this condition. But there are many other ways—such, for example, as this:—
Here, again, no barrel has a smaller number than itself on its right or
beneath it. The puzzle is to discover in how many different ways the merchant of
Bagdad might have arranged his barrels in the two rows without breaking his
rule. Can you count the number of ways?
Solution 280.—BUILDING
THE TETRAHEDRON.
I possess a tetrahedron, or triangular pyramid, formed of six sticks glued
together, as shown in the illustration. Can you count correctly the number of
different ways in which these six sticks might have been stuck together so as to
form the pyramid?
Some friends worked at it together one evening, each person providing himself
with six lucifer matches to aid his thoughts; but it was found that no two
results were the same. You see, if we remove one of the sticks and turn it round
the other way, that will be a different pyramid. If we make two of the sticks
change places the
result will again be different. But remember that every pyramid may be made to
stand on either of its four sides without being a different one. How many ways
are there altogether?
Solution 281.—PAINTING
A PYRAMID.
This puzzle concerns the painting of the four sides of a tetrahedron, or
triangular pyramid. If you cut out a piece of cardboard of the triangular shape
shown in Fig. 1, and then cut half through along the dotted lines, it will fold
up and form a perfect triangular pyramid. And I would first remind my readers
that the primary colours of the solar spectrum are seven—violet, indigo, blue,
green, yellow, orange, and red. When I was a child I was taught to remember
these by the ungainly word formed by the initials of the colours, "Vibgyor."
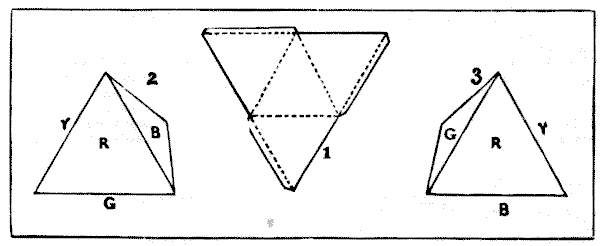
In how many different ways may the triangular pyramid be coloured, using in
every case one, two, three, or four colours of the solar spectrum? Of course a
side can only receive a single colour, and no side can be left uncoloured. But
there is one point that I must make quite clear. The four sides are not to be
regarded as individually distinct. That is to say, if you paint your pyramid as
shown in Fig. 2 (where the bottom side is green and the other side that is out
of view is yellow), and then paint another in the order shown in Fig. 3, these
are really both the same and count as one way. For if you tilt over No. 2 to the
right it will so fall as to represent No. 3. The avoidance of repetitions of
this kind is the real puzzle of the thing. If a coloured pyramid cannot be
placed so that it exactly resembles in its colours and their relative order
another pyramid, then they are different. Remember that one way would be to
colour all the four sides red, another to colour two sides green, and the
remaining sides yellow and blue; and so on.
Solution 282.—THE
ANTIQUARY'S CHAIN.
An antiquary possessed a number of curious old links, which he took to a
blacksmith, and told him to join together to form one straight piece of chain,
with the sole condition that the two circular links were not to be together. The
following illustration shows the appearance of the chain and the form of each
link. Now, supposing the owner should separate the links again, and then take
them to another smith and repeat his former instructions exactly, what are the
chances against the links being put together exactly as they were by the first
man? Remember that every successive link can be joined on to another in one of
two ways, just as you can put a ring on your finger in two ways, or link your
forefingers and thumbs in two ways.
Solution 283.—THE
FIFTEEN DOMINOES.
In this case we do not use the complete set of twenty-eight dominoes to be
found in the ordinary box. We dispense with all those dominoes that have a five or a
six on them and limit ourselves to the fifteen that remain, where the
double-four is the highest.
In how many different ways may the fifteen dominoes be arranged in a straight
line in accordance with the simple rule of the game that a number must always be
placed against a similar number—that is, a four against a four, a blank against
a blank, and so on? Left to right and right to left of the same arrangement are
to be counted as two different ways.
Solution 284.—THE
CROSS TARGET.
In the illustration we have a somewhat curious target designed by an
eccentric sharpshooter. His idea was that in order to score you must hit four
circles in as many shots so that those four shots shall form a square. It will
be seen by the results recorded on the target that two attempts have been
successful. The first man hit the four circles at the top of the cross, and thus
formed his square. The second man intended to hit the four in the bottom arm,
but his second shot, on the left, went too high. This compelled him to complete
his four in a different way than he intended. It will thus be seen that though
it is immaterial which circle you hit at the first shot, the second shot may
commit you to a definite procedure if you are to get your square. Now, the
puzzle is to say in just how many different ways it is possible to form a square
on the target with four shots.
Solution 285.—THE
FOUR POSTAGE STAMPS.
"It is as easy as counting," is an expression one sometimes hears. But mere
counting may be puzzling at times. Take the following simple example. Suppose
you have just bought twelve postage stamps, in this form—three by four—and a
friend asks you to oblige him with four stamps, all joined together—no stamp
hanging on by a mere corner. In how many different ways is it possible for you
to tear off those four stamps? You see, you can give him 1, 2, 3, 4, or 2, 3, 6,
7, or 1, 2, 3, 6, or 1, 2, 3, 7, or 2, 3, 4, 8, and so on. Can you count the
number of different ways in which those four stamps might be delivered? There
are not many more than fifty ways, so it is not a big count. Can you get the
exact number?
Solution 286.—PAINTING
THE DIE.
In how many different ways may the numbers on a single die be marked, with
the only condition that the 1 and 6, the 2 and 5, and the 3 and 4 must be on
opposite sides? It is a simple enough question, and yet it will puzzle a good
many people.
Solution 287.—AN
ACROSTIC PUZZLE.
In the making or solving of double acrostics, has it ever occurred to you to
consider the variety and limitation of the pair of initial and final letters
available for cross words? You may have to find a word beginning with A and
ending with B, or A and C, or A and D, and so on. Some combinations are
obviously impossible—such, for example, as those with Q at the end. But let us
assume that a good English word can be found for every case. Then how many
possible pairs of letters are available?
Solution
Previous Next
|