|
DISSECTION
PUZZLES.
"Take him and cut him out in little stars."
Romeo and Juliet, iii. 2.
Puzzles have infinite variety, but perhaps there is no class more ancient
than dissection, cutting-out, or superposition puzzles. They were certainly
known to the Chinese several thousand years before the Christian era. And they
are just as fascinating to-day as they can have been at any period of their
history. It is supposed by those who have investigated the matter that the
ancient Chinese philosophers used these puzzles as a sort of kindergarten method of imparting
the principles of geometry. Whether this was so or not, it is certain that all
good dissection puzzles (for the nursery type of jig-saw puzzle, which merely
consists in cutting up a picture into pieces to be put together again, is not
worthy of serious consideration) are really based on geometrical laws. This
statement need not, however, frighten off the novice, for it means little more
than this, that geometry will give us the "reason why," if we are interested in
knowing it, though the solutions may often be discovered by any intelligent
person after the exercise of patience, ingenuity, and common sagacity.
If we want to cut one plane figure into parts that by readjustment will form
another figure, the first thing is to find a way of doing it at all, and then to
discover how to do it in the fewest possible pieces. Often a dissection problem
is quite easy apart from this limitation of pieces. At the time of the
publication in the Weekly Dispatch, in 1902, of a method of cutting an
equilateral triangle into four parts that will form a square (see No. 26,
"Canterbury Puzzles"), no geometrician would have had any difficulty in doing
what is required in five pieces: the whole point of the discovery lay in
performing the little feat in four pieces only.
Mere approximations in the case of these problems are valueless; the solution
must be geometrically exact, or it is not a solution at all. Fallacies are
cropping up now and again, and I shall have occasion to refer to one or two of
these. They are interesting merely as fallacies. But I want to say something on
two little points that are always arising in cutting-out puzzles—the questions
of "hanging by a thread" and "turning over." These points can best be
illustrated by a puzzle that is frequently to be found in the old books, but
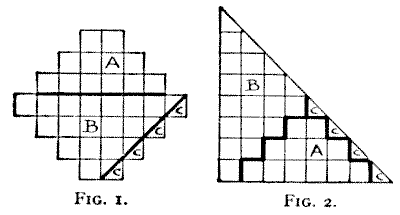
invariably with a false solution. The puzzle is to cut the figure shown in Fig.
1 into three pieces that will fit together and form a half-square triangle. The
answer that is invariably given is that shown in Figs. 1 and 2. Now, it is
claimed that the four pieces marked C are really only one piece, because they
may be so cut that they are left "hanging together by a mere thread." But no
serious puzzle lover will ever admit this. If the cut is made so as to leave the
four pieces joined in one, then it cannot result in a perfectly exact solution.
If, on the other hand, the solution is to be exact, then there will be four
pieces—or six pieces in all. It is, therefore, not a solution in three
pieces.
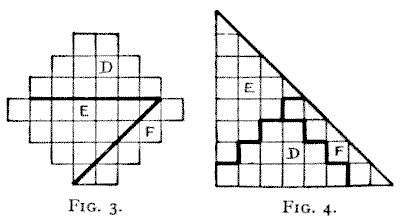
If, however, the reader will look at the solution in Figs. 3 and 4, he will
see that no such fault can be found with it. There is no question whatever that
there are three pieces, and the solution is in this respect quite satisfactory.
But another question arises. It will be found on inspection that the piece
marked F, in Fig. 3, is turned over in Fig. 4—that is to say, a different side
has necessarily to be presented. If the puzzle were merely to be cut out of
cardboard or wood, there might be no objection to this reversal, but it is quite
possible that the material would not admit of being reversed. There might be a
pattern, a polish, a difference of texture, that prevents it. But it is
generally understood that in dissection puzzles you are allowed to turn pieces
over unless it is distinctly stated that you may not do so. And very often a
puzzle is greatly improved by the added condition, "no piece may be turned
over." I have often made puzzles, too, in which the diagram has a small repeated
pattern, and the pieces have then so to be cut that not only is there no turning
over, but the pattern has to be matched, which cannot be done if the pieces are
turned round, even with the proper side uppermost.
Before presenting a varied series of cutting-out puzzles, some very easy and
others difficult, I propose to consider one family alone—those problems
involving what is known as the Greek cross with the square. This will exhibit a
great variety of curious transpositions, and, by having the solutions as we go
along, the reader will be saved the trouble of perpetually turning to another
part of the book, and will have everything under his eye. It is hoped that in
this way the article may prove somewhat instructive to the novice and
interesting to others.
Previous Next
|