|
GREEK
CROSS PUZZLES.
"To fret thy soul with crosses."
SPENSER.
"But, for my part, it was Greek to me."
Julius Cæsar, i. 2.
Many people are accustomed to consider the cross as a wholly Christian
symbol. This is erroneous: it is of very great antiquity. The ancient Egyptians
employed it as a sacred symbol, and on Greek sculptures we find representations
of a cake (the supposed real origin of our hot cross buns) bearing a cross. Two
such cakes were discovered at Herculaneum. Cecrops offered to Jupiter Olympus a
sacred cake or boun of this kind. The cross and ball, so frequently found
on Egyptian figures, is a circle and the tau cross. The circle signified
the eternal preserver of the world, and the T, named from the Greek letter
tau, is the monogram of Thoth, the Egyptian Mercury, meaning wisdom. This
tau cross is also called by Christians the cross of St. Anthony, and is
borne on a badge in the bishop's palace at Exeter. As for the Greek or mundane
cross, the cross with four equal arms, we are told by competent antiquaries that
it was regarded by ancient occultists for thousands of years as a sign of the
dual forces of Nature—the male and female spirit of everything that was
everlasting.
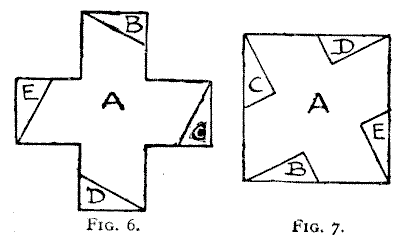
The Greek cross, as shown in Fig. 5, is formed by the assembling together of
five equal squares. We will start with what is known as the Hindu problem,
supposed to be upwards of three thousand years old. It appears in the seal of
Harvard College, and is often given in old works as symbolical of mathematical
science and exactitude. Cut the cross into five pieces to form a square. Figs. 6
and 7 show how this is done. It was not until the middle of the nineteenth
century that we found that the cross might be transformed into a square in only
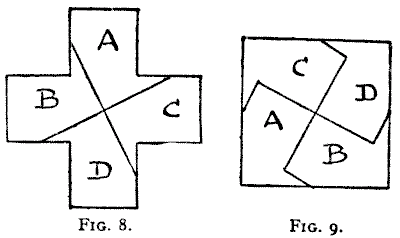
four pieces. Figs. 8 and 9 will show how to do it, if we further require the
four pieces to be all of the same size and shape. This Fig. 9 is remarkable
because, according to Dr. Le Plongeon and others, as expounded in a work by
Professor Wilson of the Smithsonian Institute, here we have the great Swastika,
or sign, of "good luck to you "—the most ancient symbol of the human race of
which there is any record. Professor Wilson's work gives some four hundred
illustrations of this curious sign as found in the Aztec mounds of Mexico, the
pyramids of Egypt, the ruins of Troy, and the ancient lore of India and China.
One might almost say there is a curious affinity between the Greek cross and
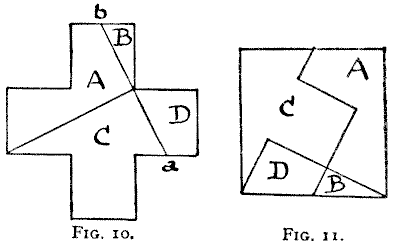
Swastika! If, however, we require that the four pieces shall be produced by only
two clips of the scissors (assuming the puzzle is in paper form), then we must
cut as in Fig. 10 to form Fig. 11, the first clip of the scissors being from
a to b. Of course folding the paper, or holding the pieces
together after the first cut, would not in this case be allowed. But there is an
infinite number of different ways of making the cuts to solve the puzzle in four
pieces. To this point I propose to return.
It will be seen that every one of these puzzles has its reverse puzzle—to cut
a square into pieces to form a Greek cross. But as a square has not so many
angles as the cross, it is not always equally easy to discover the true
directions of the cuts. Yet in the case of the examples given, I will leave the
reader to determine their direction for himself, as they are rather obvious from
the diagrams.
Cut a square
into five pieces that will form two separate Greek crosses of different
sizes. This is quite an easy puzzle. As will be seen in Fig. 12, we have
only to divide our square into 25 little squares and then cut as shown. The
cross A is cut out entire, and the pieces B, C, D, and E form the larger cross
in Fig. 13. The reader may here like to cut the single piece, B, into four
pieces all similar in shape to itself, and form a cross with them in the manner
shown in Fig. 13. I hardly need give the solution.
Cut a square into five pieces that will form two separate Greek crosses of
exactly the same size. This is more difficult. We make the cuts as in
Fig. 14, where the cross A comes out entire and the other four pieces form the
cross in Fig. 15. The direction of the cuts is pretty obvious. It will be seen
that the sides of the square in Fig. 14 are marked off into six equal parts. The
sides of the cross are found by ruling lines from certain of these points to
others.
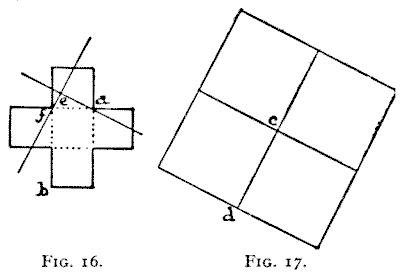
I will now explain, as I promised, why a Greek cross may be cut into four
pieces in an infinite number of different ways to make a square. Draw a cross,
as in Fig. 16. Then draw on transparent paper the square shown in Fig. 17,
taking care that the distance c to d is exactly the same as the
distance a to b in the cross. Now place the transparent paper over
the cross and slide it about into different positions, only be very careful
always to keep the square at the same angle to the cross as shown, where
a b is parallel to c d. If you place the point
c exactly over a the lines will indicate the solution (Figs. 10
and 11). If you place c in the very centre of the dotted square, it will
give the solution in Figs. 8 and 9. You will now see that by sliding the square
about so that the point c is always within the dotted square you may get
as many different solutions as you like; because, since an infinite number of
different points may theoretically be placed within this square, there must be
an infinite number of different solutions. But the point c need not
necessarily be placed within the dotted square. It may be placed, for example,
at point e to give a solution in four pieces. Here the joins at a
and f may be as slender as you like. Yet if you once get over the edge at
a or f you no longer have a solution in four pieces. This proof
will be found both entertaining and instructive. If you do not happen to have
any transparent paper at hand, any thin paper will of course do if you hold the
two sheets against a pane of glass in the window.
It may have been noticed from the solutions of the puzzles that I have given
that the side of the square formed from the cross is always equal to the
distance a to b in Fig. 16. This must necessarily be so, and I
will presently try to make the point quite clear.
We will now go one step further. I have already said that the ideal solution
to a cutting-out puzzle is always that which requires the fewest possible
pieces. We have just seen that two crosses of the same size may be cut out of a
square in five pieces. The reader who succeeded in solving this perhaps asked
himself: "Can it be done in fewer pieces?" This is just the sort of question
that the true puzzle lover is always asking, and it is the right attitude for
him to adopt. The answer to the question is that the puzzle may be solved in
four pieces—the fewest possible. This, then, is a new puzzle. Cut a square into
four pieces that will form two Greek crosses of the same size.
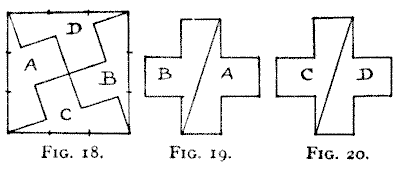
The solution is very beautiful. If you divide by points the sides of the
square into three equal parts, the directions of the lines in Fig. 18 will be
quite obvious. If you cut along these lines, the pieces A and B will form the cross in
Fig. 19 and the pieces C and D the similar cross in Fig. 20. In this square we
have another form of Swastika.
The reader will here appreciate the truth of my remark to the effect that it
is easier to find the directions of the cuts when transforming a cross to a
square than when converting a square into a cross. Thus, in Figs. 6, 8, and 10
the directions of the cuts are more obvious than in Fig. 14, where we had first
to divide the sides of the square into six equal parts, and in Fig. 18, where we
divide them into three equal parts. Then, supposing you were required to cut two
equal Greek crosses, each into two pieces, to form a square, a glance at Figs.
19 and 20 will show how absurdly more easy this is than the reverse puzzle of
cutting the square to make two crosses.
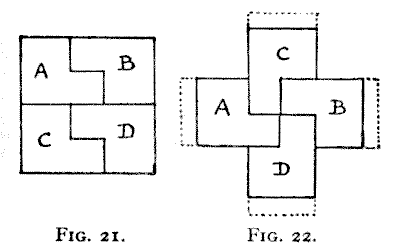
Referring to my remarks on "fallacies," I will now give a little example of
these "solutions" that are not solutions. Some years ago a young correspondent
sent me what he evidently thought was a brilliant new discovery—the transforming
of a square into a Greek cross in four pieces by cuts all parallel to the sides
of the square. I give his attempt in Figs. 21 and 22, where it will be seen that
the four pieces do not form a symmetrical Greek cross, because the four arms are
not really squares but oblongs. To make it a true Greek cross we should require
the additions that I have indicated with dotted lines. Of course his solution
produces a cross, but it is not the symmetrical Greek variety required by the
conditions of the puzzle. My young friend thought his attempt was "near enough"
to be correct; but if he bought a penny apple with a sixpence he probably would
not have thought it "near enough" if he had been given only fourpence change. As
the reader advances he will realize the importance of this question of
exactitude.
In these cutting-out puzzles it is necessary not only to get the directions
of the cutting lines as correct as possible, but to remember that these lines
have no width. If after cutting up one of the crosses in a manner indicated in
these articles you find that the pieces do not exactly fit to form a square, you
may be certain that the fault is entirely your own. Either your cross was not
exactly drawn, or your cuts were not made quite in the right directions, or (if
you used wood and a fret-saw) your saw was not sufficiently fine. If you cut out
the puzzles in paper with scissors, or in cardboard with a penknife, no material
is lost; but with a saw, however fine, there is a certain loss. In the case of
most puzzles this slight loss is not sufficient to be appreciable, if the puzzle
is cut out on a large scale, but there have been instances where I have found it
desirable to draw and cut out each part separately—not from one diagram—in order
to produce a perfect result.
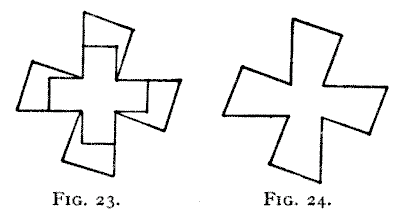
Now for another puzzle. If you have cut out the five pieces indicated in Fig.
14, you will find that these can be put together so as to form the curious cross
shown in Fig. 23. So if I asked you to cut Fig. 24 into five pieces to form
either a square or two equal Greek crosses you would know how to do it. You
would make the cuts as in Fig. 23, and place them together as in Figs. 14 and
15. But I want something better than that, and it is this. Cut Fig. 24 into only
four pieces that will fit together and form a square.
The solution to the puzzle is shown in Figs. 25 and 26. The direction of the
cut dividing A and C in the first diagram is very obvious, and the second cut is
made at right angles to it. That the four pieces should fit together and form a
square will surprise the novice, who will do well to study the puzzle with some
care, as it is most instructive.
I will now explain the beautiful rule by which we determine the size of a
square that shall have the same area as a Greek cross, for it is applicable, and
necessary, to the solution of almost every dissection puzzle that we meet with.
It was first discovered by the philosopher Pythagoras, who died 500 B.C., and is
the 47th proposition of Euclid. The young reader who knows nothing of the
elements of geometry will get some idea of the fascinating character of that
science. The triangle ABC in Fig. 27 is what we call a right-angled triangle,
because the side BC is at right angles to the side AB. Now if we build up a
square on each side of the triangle, the squares on AB and BC will together be exactly
equal to the square on the long side AC, which we call the hypotenuse. This is
proved in the case I have given by subdividing the three squares into cells of
equal dimensions.
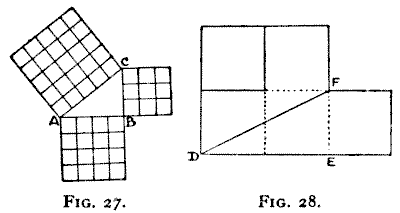
It will be seen that 9 added to 16 equals 25, the number of cells in the
large square. If you make triangles with the sides 5, 12 and 13, or with 8, 15
and 17, you will get similar arithmetical proofs, for these are all "rational"
right-angled triangles, but the law is equally true for all cases. Supposing we
cut off the lower arm of a Greek cross and place it to the left of the upper
arm, as in Fig. 28, then the square on EF added to the square on DE exactly
equals a square on DF. Therefore we know that the square of DF will contain the
same area as the cross. This fact we have proved practically by the solutions of
the earlier puzzles of this series. But whatever length we give to DE and EF, we
can never give the exact length of DF in numbers, because the triangle is not a
"rational" one. But the law is none the less geometrically true.
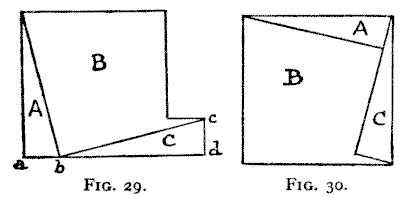
Now look at Fig. 29, and you will see an elegant method for cutting a piece
of wood of the shape of two squares (of any relative dimensions) into three
pieces that will fit together and form a single square. If you mark off the
distance ab equal to the side cd the directions of the cuts are
very evident. From what we have just been considering, you will at once see why
bc must be the length of the side of the new square. Make the experiment
as often as you like, taking different relative proportions for the two squares,
and you will find the rule always come true. If you make the two squares of
exactly the same size, you will see that the diagonal of any square is always
the side of a square that is twice the size. All this, which is so simple that
anybody can understand it, is very essential to the solving of cutting-out
puzzles. It is in fact the key to most of them. And it is all so beautiful that
it seems a pity that it should not be familiar to everybody.

We will now go one step further and deal with the half-square. Take a square
and cut it in half diagonally. Now try to discover how to cut this triangle into
four pieces that will form a Greek cross. The solution is shown in Figs. 31 and
32. In this case it will be seen that we divide two of the sides of the triangle
into three equal parts and the long side into four equal parts. Then the
direction of the cuts will be easily found. It is a pretty puzzle, and a little
more difficult than some of the others that I have given. It should be noted
again that it would have been much easier to locate the cuts in the reverse
puzzle of cutting the cross to form a half-square triangle.

Another ideal that the puzzle maker always keeps in mind is to contrive that
there shall, if possible, be only one correct solution. Thus, in the case of the
first puzzle, if we only require that a Greek cross shall be cut into four
pieces to form a square, there is, as I have shown, an infinite number of
different solutions. It makes a better puzzle to add the condition that all the
four pieces shall be of the same size and shape, because it can then be solved
in only one way, as in Figs. 8 and 9. In this way, too, a puzzle that is too
easy to be interesting may be improved by such an addition. Let us take an
example. We have seen in Fig. 28 that Fig. 33 can be cut into two pieces to form
a Greek cross. I suppose an intelligent child would do it in five minutes. But
suppose we say that the puzzle has to be solved with a piece of wood that has
a bad knot in the
position shown in Fig. 33—a knot that we must not attempt to cut through—then a
solution in two pieces is barred out, and it becomes a more interesting puzzle
to solve it in three pieces. I have shown in Figs. 33 and 34 one way of doing
this, and it will be found entertaining to discover other ways of doing it. Of
course I could bar out all these other ways by introducing more knots, and so
reduce the puzzle to a single solution, but it would then be overloaded with
conditions.
And this brings us to another point in seeking the ideal. Do not overload
your conditions, or you will make your puzzle too complex to be interesting. The
simpler the conditions of a puzzle are, the better. The solution may be as
complex and difficult as you like, or as happens, but the conditions ought to be
easily understood, or people will not attempt a solution.
If the reader were now asked "to cut a half-square into as few pieces as
possible to form a Greek cross," he would probably produce our solution, Figs.
31-32, and confidently claim that he had solved the puzzle correctly. In this
way he would be wrong, because it is not now stated that the square is to be
divided diagonally. Although we should always observe the exact conditions of a
puzzle we must not read into it conditions that are not there. Many puzzles are
based entirely on the tendency that people have to do this.
The very first essential in solving a puzzle is to be sure that you
understand the exact conditions. Now, if you divided your square in half so as
to produce Fig. 35 it is possible to cut it into as few as three pieces to form
a Greek cross. We thus save a piece.
I give another puzzle in Fig. 36. The dotted lines are added merely to show
the correct proportions of the figure—a square of 25 cells with the four corner
cells cut out. The puzzle is to cut this figure into five pieces that will form
a Greek cross (entire) and a square.
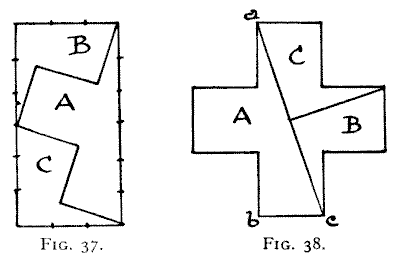
The solution to the first of the two puzzles last given—to cut a rectangle of
the shape of a half-square into three pieces that will form a Greek cross—is
shown in Figs. 37 and 38. It will be seen that we divide the long sides of the
oblong into six equal parts and the short sides into three equal parts, in order
to get the points that will indicate the direction of the cuts. The reader
should compare this solution with some of the previous illustrations. He will
see, for example, that if we continue the cut that divides B and C in the cross,
we get Fig. 15.
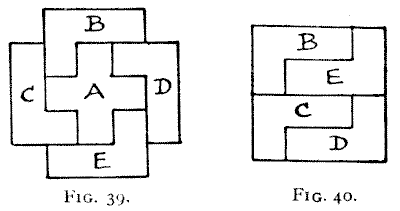
The other puzzle, like the one illustrated in Figs. 12 and 13, will show how
useful a little arithmetic may sometimes prove to be in the solution of
dissection puzzles. There are twenty-one of those little square cells into which
our figure is subdivided, from which we have to form both a square and a Greek
cross. Now, as the cross is built up of five squares, and 5 from 21 leaves 16—a
square number—we ought easily to be led to the solution shown in Fig. 39. It
will be seen that the cross is cut out entire, while the four remaining pieces
form the square in Fig. 40.
Of course a half-square rectangle is the same as a double square, or two
equal squares joined together. Therefore, if you want to solve the puzzle of
cutting a Greek cross into four pieces to form two separate squares of the same
size, all you have to do is to continue the short cut in Fig. 38 right across
the cross, and you will have four pieces of the same size and shape. Now divide
Fig. 37 into two equal squares by a horizontal cut midway and you will see the
four pieces forming the two squares.
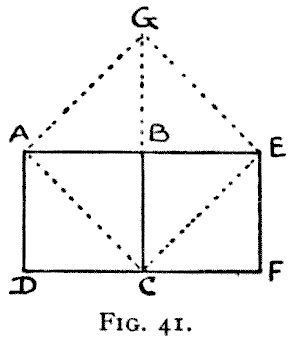
Cut a Greek
cross into five pieces that will form two separate squares, one of which shall
contain half the area of one of the arms of the cross. In further illustration
of what I have already written, if the two squares of the same size A B C D and
B C F E, in Fig. 41, are cut in the manner indicated by the dotted lines, the
four pieces will form the large square A G E C. We thus see that the diagonal A
C is the side of a square twice the size of A B C D. It is also clear that half
the diagonal of any square is equal to the side of a square of half the area.
Therefore, if the large square in the diagram is one of the arms of your cross,
the small square is the size of one of the squares required in the puzzle.
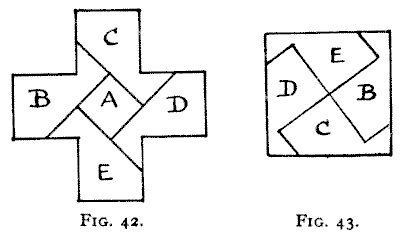
The solution is shown in Figs. 42 and 43. It will be seen that the small
square is cut out whole and the large square composed of the four pieces B, C,
D, and E. After what I have written, the reader will have no difficulty in
seeing that the square A is half the size of one of the arms of the cross,
because the length of the diagonal of the former is clearly the same as the side
of the latter. The thing is now self-evident. I have thus tried to show that
some of these puzzles that many people are apt to regard as quite wonderful and
bewildering, are really not difficult if only we use a little thought and
judgment. In conclusion of this particular subject I will give four Greek cross
puzzles, with detached solutions.
142.—THE
SILK PATCHWORK.
The lady members of the Wilkinson family had made a simple patchwork quilt,
as a small Christmas present, all composed of square pieces of the same size, as
shown in the illustration. It only lacked the four corner pieces to make it
complete. Somebody pointed out to them that if you unpicked the Greek cross in
the middle and then cut the stitches along the dark joins, the four pieces all
of the same size and shape would fit together and form a square. This the reader
knows, from the solution in Fig. 39, is quite easily done. But George Wilkinson
suddenly suggested to them this poser. He said, "Instead of picking out the
cross entire, and forming the square from four equal pieces, can you cut out a
square entire and four equal pieces that will form a perfect Greek cross?" The
puzzle is, of course, now quite easy.
Solution
143.—TWO
CROSSES FROM ONE.
Cut a Greek cross into five pieces that will form two such crosses, both of
the same size. The solution of this puzzle is very beautiful.
Solution
144.—THE
CROSS AND THE TRIANGLE.
Cut a Greek cross into six pieces that will form an equilateral triangle.
This is another hard problem, and I will state here that a solution is
practically impossible without a previous knowledge of my method of transforming
an equilateral triangle into a square (see No. 26, "Canterbury Puzzles").
Solution
145.—THE
FOLDED CROSS.
Cut out of paper a Greek cross; then so fold it that with a single straight
cut of the scissors the four pieces produced will form a square.
Solution
Previous Next
|