VARIOUS
DISSECTION PUZZLES.
We will now consider a small miscellaneous selection of cutting-out puzzles,
varying in degrees of difficulty.
146.—AN
EASY DISSECTION PUZZLE.
First, cut out a piece of paper or cardboard of the shape shown in the
illustration. It will be seen at once that the proportions are simply those of a
square attached to half of another similar square, divided diagonally. The
puzzle is to cut it into four pieces all of precisely the same size and shape
Solution
147.—AN
EASY SQUARE PUZZLE.
If you take a rectangular piece of cardboard, twice as long as it is broad,
and cut it in half diagonally, you will get two of the pieces shown in the
illustration. The puzzle is with five such pieces of equal size to form a
square. One of the pieces may be cut in two, but the others must be used
intact.
Solution
148.—THE
BUN PUZZLE.
The three circles represent three buns, and it is simply required to show how
these may be equally divided among four boys. The buns must be regarded as of
equal thickness throughout and of equal thickness to each other. Of course, they
must be cut into as few pieces as possible. To simplify it I will state the
rather surprising fact that only five pieces are necessary, from which it will
be seen that one boy gets his share in two pieces and the other three receive
theirs in a single piece. I am aware that this statement "gives away" the
puzzle, but it should not destroy its interest to those who like to discover the
"reason why."
Solution
149.—THE
CHOCOLATE SQUARES.
Here is a slab of chocolate, indented at the dotted lines so that the twenty
squares can be easily separated. Make a copy of the slab in paper or cardboard
and then try to cut it into nine pieces so that they will form four perfect
squares all of exactly the same size.
Solution
150.—DISSECTING
A MITRE.
The figure that is perplexing the carpenter in the illustration represents a
mitre. It will be seen that its proportions are those of a square with one
quarter removed. The puzzle is to cut it into five pieces that will fit together
and form a perfect square. I show an attempt, published in America, to perform
the feat in four
pieces, based on what is known as the "step principle," but it is a fallacy.
We are told first to cut oft the pieces 1 and 2 and pack them into the
triangular space marked off by the dotted line, and so form a rectangle.
So far, so good. Now, we are directed to apply the old step principle, as
shown, and, by moving down the piece 4 one step, form the required square. But,
unfortunately, it does not produce a square: only an oblong. Call the
three long sides of the mitre 84 in. each. Then, before cutting the steps, our
rectangle in three pieces will be 84×63. The steps must be 10½ in. in height and
12 in. in breadth. Therefore, by moving down a step we reduce by 12 in. the side
84 in. and increase by 10½ in. the side 63 in. Hence our final rectangle must be
72 in. × 73½ in., which certainly is not a square! The fact is, the
step principle can only be applied to rectangles with sides of particular
relative lengths. For example, if the shorter side in this case were
615/7 (instead of 63), then the step method would apply.
For the steps would then be 102/7 in. in height and 12 in.
in breadth. Note that 615/7 × 84= the square of
72. At present no solution has been found in four pieces, and I do not believe
one possible.
Solution
151.—THE
JOINER'S PROBLEM.
I have often had occasion to remark on the practical utility of puzzles,
arising out of an application to the ordinary affairs of life of the little
tricks and "wrinkles" that we learn while solving recreation problems.
The joiner, in the illustration, wants to cut the piece of wood into as few
pieces as possible to form a square table-top, without any waste of material. How should
he go to work? How many pieces would you require?
Solution
152.—ANOTHER
JOINER'S PROBLEM.
A joiner had two pieces of wood of the shapes and relative proportions shown
in the diagram. He wished to cut them into as few pieces as possible so that
they could be fitted together, without waste, to form a perfectly square
table-top. How should he have done it? There is no necessity to give
measurements, for if the smaller piece (which is half a square) be made a little
too large or a little too small it will not affect the method of solution.
Solution
153.—A
CUTTING-OUT PUZZLE.
Here is a little cutting-out poser. I take a strip of paper, measuring five
inches by one inch, and, by cutting it into five pieces, the parts fit together
and form a square, as shown in the illustration. Now, it is quite an interesting
puzzle to discover how we can do this in only four pieces.
Solution
154.—MRS.
HOBSON'S HEARTHRUG.
Mrs. Hobson's boy had an accident when playing with the fire, and burnt two
of the corners of a pretty hearthrug. The damaged corners have been cut away,
and it now has the appearance and proportions shown in my diagram. How is Mrs.
Hobson to cut the rug into the fewest possible pieces that will fit together and
form a perfectly square rug? It will be seen that the rug is in the proportions
36 × 27 (it does not matter whether we say inches or yards), and each
piece cut away measured 12 and 6 on the outside.
Solution
155.—THE
PENTAGON AND SQUARE.
I wonder how many of my readers, amongst those who have not given any close
attention to the elements of geometry, could draw a regular pentagon, or
five-sided figure, if they suddenly required to do so. A regular hexagon, or
six-sided figure, is easy enough, for everybody knows that all you have to do is
to describe a circle and then, taking the radius as the length of one of the
sides, mark off the six points round the circumference. But a pentagon is quite
another matter. So, as my puzzle has to do with the cutting up of a regular
pentagon, it will perhaps be well if I first show my less experienced readers
how this figure is to be correctly drawn. Describe a circle and draw the two
lines H B and D G, in the diagram, through the centre at right angles. Now find
the point A, midway between C and B. Next place the point of your compasses at A
and with the
distance A D describe the arc cutting H B at E. Then place the point of your
compasses at D and with the distance D E describe the arc cutting the
circumference at F. Now, D F is one of the sides of your pentagon, and you have
simply to mark off the other sides round the circle. Quite simple when you know
how, but otherwise somewhat of a poser.
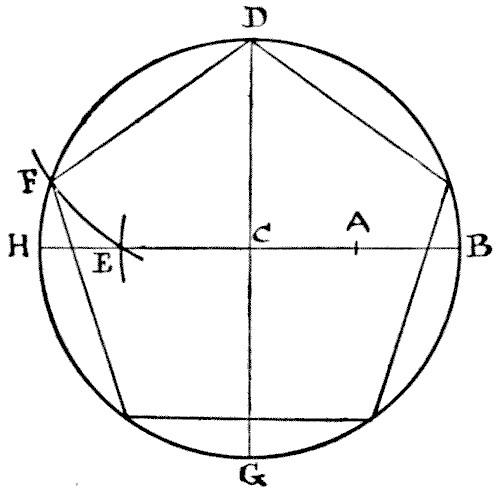
Having formed your pentagon, the puzzle is to cut it into the fewest possible
pieces that will fit together and form a perfect square.
Solution
156.—THE
DISSECTED TRIANGLE.
A good puzzle is that which the gentleman in the illustration is showing to
his friends. He has simply cut out of paper an equilateral triangle—that is, a
triangle with all its three sides of the same length. He proposes that it shall
be cut into five pieces in such a way that they will fit together and form
either two or three smaller equilateral triangles, using all the material in
each case. Can you discover how the cuts should be made?
Remember that when you have made your five pieces, you must be able, as
desired, to put them together to form either the single original triangle or to
form two triangles or to form three triangles—all equilateral.
Solution
157.—THE
TABLE-TOP AND STOOLS.
I have frequently had occasion to show that the published answers to a great
many of the oldest and most widely known puzzles are either quite incorrect or
capable of improvement. I propose to consider the old poser of the table-top and
stools that most of my readers have probably seen in some form or another in
books compiled for the recreation of childhood.
The story is told that an economical and ingenious schoolmaster once wished
to convert a circular table-top, for which he had no use, into seats for two
oval stools, each with a hand-hole in the centre. He instructed the carpenter to
make the cuts as in the illustration and then join the eight pieces together in
the manner shown. So impressed was he with the ingenuity of his performance that
he set the puzzle to his geometry class as a little study in dissection. But the
remainder of the story has never been published, because, so it is said, it was
a characteristic of the principals of academies that they would never admit that
they could err. I get my information from a descendant of the original boy who had most
reason to be interested in the matter.
The clever youth suggested modestly to the master that the hand-holes were
too big, and that a small boy might perhaps fall through them. He therefore
proposed another way of making the cuts that would get over this objection. For
his impertinence he received such severe chastisement that he became convinced
that the larger the hand-hole in the stools the more comfortable might they
be.
Now what was the method the boy proposed?
Can you show how the circular table-top may be cut into eight pieces that
will fit together and form two oval seats for stools (each of exactly the same
size and shape) and each having similar hand-holes of smaller dimensions than in
the case shown above? Of course, all the wood must be used.
Solution
158.—THE
GREAT MONAD.

Here is a symbol of tremendous antiquity which is worthy of notice. It is
borne on the Korean ensign and merchant flag, and has been adopted as a trade
sign by the Northern Pacific Railroad Company, though probably few are aware
that it is the Great Monad, as shown in the sketch below. This sign is to the
Chinaman what the cross is to the Christian. It is the sign of Deity and
eternity, while the two parts into which the circle is divided are called the
Yin and the Yan—the male and female forces of nature. A writer on the subject
more than three thousand years ago is reported to have said in reference to it:
"The illimitable produces the great extreme. The great extreme produces the two
principles. The two principles produce the four quarters, and from the four
quarters we develop the quadrature of the eight diagrams of Feuh-hi." I hope
readers will not ask me to explain this, for I have not the slightest idea what
it means. Yet I am persuaded that for ages the symbol has had occult and
probably mathematical meanings for the esoteric student.
I will introduce the Monad in its elementary form. Here are three easy
questions respecting this great symbol:—
(I.) Which has the greater area, the inner circle containing the Yin and the
Yan, or the outer ring?
(II.) Divide the Yin and the Yan into four pieces of the same size and shape
by one cut.
(III.) Divide the Yin and the Yan into four pieces of the same size, but
different shape, by one straight cut.
Solution
159.—THE
SQUARE OF VENEER.
The following represents a piece of wood in my possession, 5 in. square. By
markings on the surface it is divided into twenty-five square inches. I want to
discover a way of cutting this piece of wood into the fewest possible pieces
that will fit together and form two perfect squares of different sizes and of
known dimensions. But, unfortunately, at every one of the sixteen intersections
of the cross lines a small nail has been driven in at some time or other, and my
fret-saw will be injured if it comes in contact with any of these. I have therefore to find a
method of doing the work that will not necessitate my cutting through any of
those sixteen points. How is it to be done? Remember, the exact dimensions of
the two squares must be given.
Solution
160.—THE
TWO HORSESHOES.
Why horseshoes should be considered "lucky" is one of those things which no
man can understand. It is a very old superstition, and John Aubrey (1626-1700)
says, "Most houses at the West End of London have a horseshoe on the threshold."
In Monmouth Street there were seventeen in 1813 and seven so late as 1855. Even
Lord Nelson had one nailed to the mast of the ship Victory. To-day we
find it more conducive to "good luck" to see that they are securely nailed on
the feet of the horse we are about to drive.
Nevertheless, so far as the horseshoe, like the Swastika and other emblems
that I have had occasion at times to deal with, has served to symbolize health,
prosperity, and goodwill towards men, we may well treat it with a certain amount
of respectful interest. May there not, moreover, be some esoteric or lost
mathematical mystery concealed in the form of a horseshoe? I have been looking
into this matter, and I wish to draw my readers' attention to the very
remarkable fact that the pair of horseshoes shown in my illustration are related
in a striking and beautiful manner to the circle, which is the symbol of
eternity. I present this fact in the form of a simple problem, so that it may be
seen how subtly this relation has been concealed for ages and ages. My readers
will, I know, be pleased when they find the key to the mystery.
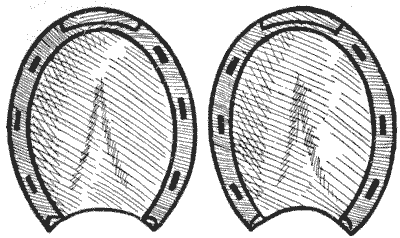
Cut out the two horseshoes carefully round the outline and then cut them into
four pieces, all different in shape, that will fit together and form a perfect
circle. Each shoe must be cut into two pieces and all the part of the horse's
hoof contained within the outline is to be used and regarded as part of the
area.
Solution
161.—THE
BETSY ROSS PUZZLE.
A correspondent asked me to supply him with the solution to an old puzzle
that is attributed to a certain Betsy Ross, of Philadelphia, who showed it to
George Washington. It consists in so folding a piece of paper that with one clip
of the scissors a five-pointed star of Freedom may be produced. Whether the
story of the puzzle's origin is a true one or not I cannot say, but I have a
print of the old house in Philadelphia where the lady is said to have lived, and
I believe it still stands there. But my readers will doubtless be interested in
the little poser.
Take a circular piece of paper and so fold it that with one cut of the
scissors you can produce a perfect five-pointed star.
Solution
162.—THE
CARDBOARD CHAIN.
Can you cut this chain out of a piece of cardboard without any join whatever?
Every link is solid; without its having been split and afterwards joined at any
place. It is an interesting old puzzle that I learnt as a child, but I have no
knowledge as to its inventor.
Solution
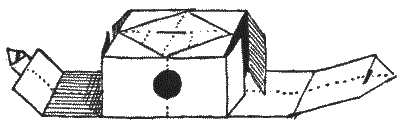
163.—THE
PAPER BOX.
It may be interesting to introduce here, though it is not strictly a puzzle,
an ingenious method for making a paper box.
Take a square of stout paper and by successive foldings make all the creases
indicated by the dotted lines in the illustration. Then cut away the eight
little triangular pieces that are shaded, and cut through the paper along the
dark lines. The second illustration shows the box half folded up, and the reader
will have no difficulty in effecting its completion. Before folding up, the
reader might cut out the circular piece indicated in the diagram, for a purpose
I will now explain.

This box will be found to serve excellently for the production of vortex
rings. These rings, which were discussed by Von Helmholtz in 1858, are most
interesting, and the box (with the hole cut out) will produce them to
perfection. Fill the box with tobacco smoke by blowing it gently through the
hole. Now, if you hold it horizontally, and softly tap the side that is opposite
to the hole, an immense number of perfect rings can be produced from one
mouthful of smoke. It is best that there should be no currents of air in the
room. People often do not realise that these rings are formed in the air when no
smoke is used. The smoke only makes them visible. Now, one of these rings, if
properly directed on its course, will travel across the room and put out the
flame of a candle, and this feat is much more striking if you can manage to do
it without the smoke. Of course, with a little practice, the rings may be blown
from the mouth, but the box produces them in much greater perfection, and no
skill whatever is required. Lord Kelvin propounded the theory that matter may
consist of vortex rings in a fluid that fills all space, and by a development of
the hypothesis he was able to explain chemical combination.
164.—THE
POTATO PUZZLE.
Take a circular slice of potato, place it on the table, and see into how
large a number of pieces you can divide it with six cuts of a knife. Of course
you must not readjust the pieces or pile them after a cut. What is the greatest
number of pieces you can make?
The illustration shows how to make sixteen pieces. This can, of course, be
easily beaten.
Solution
165.—THE
SEVEN PIGS.
Here is a little puzzle that was put to one of the sons of Erin the other day
and perplexed him unduly, for it is really quite easy. It will be seen from the
illustration that he was shown a sketch of a square pen containing seven pigs.
He was asked how he would intersect the pen with three straight fences so as to
enclose every pig in a separate sty. In other words, all you have to do is to
take your pencil and, with three straight strokes across the square, enclose
each pig separately. Nothing could be simpler.
The Irishman complained that the pigs would not keep still while he was
putting up the fences. He said that they would all flock together, or one
obstinate beast would go into a corner and flock all by himself. It was pointed
out to him that for the purposes of the puzzle the pigs were stationary. He
answered that Irish pigs are not stationery—they are pork. Being persuaded to
make the attempt, he drew three lines, one of which cut through a pig. When it
was explained that this is not allowed, he protested that a pig was no use until you cut its
throat. "Begorra, if it's bacon ye want without cutting your pig, it will be all
gammon." We will not do the Irishman the injustice of suggesting that the
miserable pun was intentional. However, he failed to solve the puzzle. Can you
do it?
Solution
166.—THE
LANDOWNER'S FENCES.
The landowner in the illustration is consulting with his bailiff over a
rather puzzling little question. He has a large plan of one of his fields, in
which there are eleven trees. Now, he wants to divide the field into just eleven
enclosures by means of straight fences, so that every enclosure shall contain
one tree as a shelter for his cattle. How is he to do it with as few fences as
possible? Take your pencil and draw straight lines across the field until you
have marked off the eleven enclosures (and no more), and then see how many
fences you require. Of course the fences may cross one another.
Solution
167.—THE
WIZARD'S CATS.
A wizard placed ten cats inside a magic circle as shown in our illustration,
and hypnotized them so that they should remain stationary during his pleasure.
He then proposed to draw three circles inside the large one, so that no cat
could approach another cat without crossing a magic circle. Try to draw the three circles
so that every cat has its own enclosure and cannot reach another cat without
crossing a line.
Solution
168.—THE
CHRISTMAS PUDDING.
"Speaking of Christmas puddings," said the host, as he glanced at the
imposing delicacy at the other end of the table. "I am reminded of the fact that
a friend gave me a new puzzle the other day respecting one. Here it is," he
added, diving into his breast pocket.
"'Problem: To find the contents,' I suppose," said the Eton boy.
"No; the proof of that is in the eating. I will read you the conditions."
"'Cut the pudding into two parts, each of exactly the same size and shape,
without touching any of the plums. The pudding is to be regarded as a flat disc,
not as a sphere.'"
"Why should you regard a Christmas pudding as a disc? And why should any
reasonable person ever wish to make such an accurate division?" asked the
cynic.
"It is just a puzzle—a problem in dissection." All in turn had a look at the
puzzle, but nobody succeeded in solving it. It is a little difficult unless you
are acquainted with the principle involved in the making of such puddings, but
easy enough when you know how it is done.
Solution
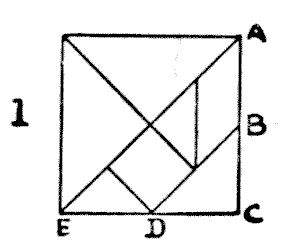
169.—A
TANGRAM PARADOX.
Many pastimes of great antiquity, such as chess, have so developed and
changed down the centuries that their original inventors would scarcely
recognize them. This is not the case with Tangrams, a recreation that appears to
be at least four thousand years old, that has apparently never been dormant, and
that has not been altered or "improved upon" since the legendary Chinaman Tan
first cut out the seven pieces shown in Diagram I. If you mark the point B,
midway between A and C, on one side of a square of any size, and D, midway
between C and E, on an adjoining side, the direction of the cuts is too obvious
to need further explanation. Every design in this article is built up from the
seven pieces of blackened cardboard. It will at once be understood that the
possible combinations are infinite.
The late Mr. Sam Loyd, of New York, who published a small book of very
ingenious designs, possessed the manuscripts of the late Mr. Challenor, who made
a long and close study of Tangrams. This gentleman, it is said, records that
there were originally seven books of Tangrams, compiled in China two thousand
years before the Christian era. These books are so rare that, after forty years'
residence in the country, he only succeeded in seeing perfect copies of the
first and seventh volumes with fragments of the second. Portions of one of the
books, printed in gold leaf upon parchment, were found in Peking by an English
soldier and sold for three hundred pounds.
A few years ago a little book came into my possession, from the library of
the late Lewis Carroll, entitled The Fashionable Chinese Puzzle. It
contains three hundred and twenty-three Tangram designs, mostly nondescript
geometrical figures, to be constructed from the seven pieces. It was "Published
by J. and E. Wallis, 42 Skinner Street, and J. Wallis, Jun., Marine Library,
Sidmouth" (South Devon). There is no date, but the following note fixes the time
of publication pretty closely: "This ingenious contrivance has for some time
past been the favourite amusement of the ex-Emperor Napoleon, who, being now in
a debilitated state and living very retired, passes many hours a day in thus
exercising his patience and ingenuity." The reader will find, as did the great
exile, that much amusement, not wholly uninstructive, may be derived from
forming the designs of others. He will find many of the illustrations to this
article quite easy to build up, and some rather difficult. Every picture may
thus be regarded as a puzzle.
But it is another pastime altogether to create new and original designs of a
pictorial character, and it is surprising what extraordinary scope the Tangrams
afford for producing pictures of real life—angular and often grotesque, it is
true, but full of character. I give an example of a recumbent figure (2) that is
particularly graceful, and only needs some slight reduction of its angularities
to produce an entirely satisfactory outline.
As I have referred to the author of Alice in Wonderland, I give also
my designs of the March Hare (3) and the Hatter (4). I also give an attempt at
Napoleon (5), and a very excellent Red Indian with his Squaw by Mr. Loyd (6 and
7). A large number of other designs will be found in an article by me in The
Strand Magazine for November, 1908.
On the appearance of this magazine article, the late Sir James Murray, the
eminent philologist, tried, with that amazing industry that characterized all
his work, to trace the word "tangram" to its source. At length he wrote as
follows:—"One of my sons is a professor in the Anglo-Chinese college at
Tientsin. Through him, his colleagues, and his students, I was able to make
inquiries as to the alleged Tan among Chinese scholars. Our Chinese professor
here (Oxford) also took an interest in the matter and obtained information from
the secretary of the Chinese Legation in London, who is a very eminent
representative of the Chinese literati."
"The result has been to show that the man Tan, the god Tan, and the 'Book of
Tan' are entirely unknown to Chinese literature, history, or tradition. By most
of the learned men the name, or allegation of the existence, of these had never
been heard of. The puzzle is, of course, well known. It is called in Chinese
ch'i ch'iao t'u; literally, 'seven-ingenious-plan' or 'ingenious-puzzle
figure of seven pieces.' No name approaching 'tangram,' or even 'tan,' occurs in
Chinese, and the only suggestions for the latter were the Chinese t'an,
'to extend'; or t'ang, Cantonese dialect for 'Chinese.' It was suggested
that probably some American or Englishman who knew a little Chinese or
Cantonese, wanting a name for the puzzle, might concoct one out of one of these
words and the European ending 'gram.' I should say the name 'tangram' was
probably invented by an American some little time before 1864 and after 1847,
but I cannot find it in print before the 1864 edition of Webster. I have
therefore had to deal very shortly with the word in the dictionary, telling what
it is applied to and what conjectures or guesses have been made at the name, and
giving a few quotations, one from your own article, which has enabled me to make
more of the subject than I could otherwise have done."
Several correspondents have informed me that they possess, or had possessed,
specimens of the old Chinese books. An American gentleman writes to me as
follows:—"I have in my possession a book made of tissue paper, printed in black
(with a Chinese inscription on the front page), containing over three hundred
designs, which belongs to the box of 'tangrams,' which I also own. The blocks
are seven in number, made of mother-of-pearl, highly polished and finely
engraved on either side. These are contained in a rosewood box
21/8 in. square. My great uncle, ——, was one of the first
missionaries to visit China. This box and book, along with quite a collection of
other relics, were sent to my grandfather and descended to myself."

My correspondent kindly supplied me with rubbings of the Tangrams, from which
it is clear that they are cut in the exact proportions that I have indicated. I
reproduce the Chinese inscription (8) for this reason. The owner of the book
informs me that he has submitted it to a number of Chinamen in the United States
and offered as much as a dollar for a translation. But they all steadfastly
refused to read the words, offering the lame excuse that the inscription is
Japanese. Natives of Japan, however, insist that it is Chinese. Is there
something occult and esoteric about Tangrams, that it is so difficult to lift the veil? Perhaps
this page will come under the eye of some reader acquainted with the Chinese
language, who will supply the required translation, which may, or may not, throw
a little light on this curious question.

By using several sets of Tangrams at the same time we may construct more
ambitious pictures. I was advised by a friend not to send my picture, "A Game of
Billiards" (9), to the Academy. He assured me that it would not be accepted
because the "judges are so hide-bound by convention." Perhaps he was right, and
it will be more appreciated by Post-impressionists and Cubists. The players are
considering a very delicate stroke at the top of the table. Of course, the two
men, the table, and the clock are formed from four sets of Tangrams. My second
picture is named "The Orchestra" (10), and it was designed for the decoration of
a large hall of music. Here we have the conductor, the pianist, the fat little
cornet-player, the left-handed player of the double-bass, whose attitude is
life-like, though he does stand at an unusual distance from his instrument, and
the drummer-boy, with his imposing music-stand. The dog at the back of the
pianoforte is not howling: he is an appreciative listener.


One remarkable thing about these Tangram pictures is that they suggest to the
imagination such a lot that is not really there. Who, for example, can look for
a few minutes at Lady Belinda (11) and the Dutch girl (12) without soon feeling
the haughty expression in the one case and the arch look in the other? Then look
again at the stork (13), and see how it is suggested to the mind that the leg is
actually much more slender than any one of the pieces employed. It is really an
optical illusion. Again, notice in the case of the yacht (14) how, by leaving
that little angular point at the top, a complete mast is suggested. If you place
your Tangrams together on white paper so that they do not quite touch one
another, in some cases the effect is improved by the white lines; in other cases
it is almost destroyed.
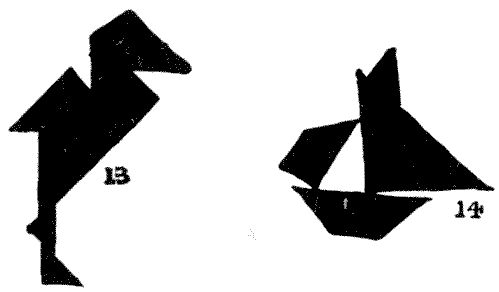
Finally, I give an example from the many curious paradoxes that one happens
upon in manipulating Tangrams. I show designs of two dignified individuals (15 and 16) who
appear to be exactly alike, except for the fact that one has a foot and the
other has not. Now, both of these figures are made from the same seven Tangrams.
Where does the second man get his foot from?
Solution
Previous Next
|