THE
CHESSBOARD.
"Good company's a chessboard."
BYRON'S Don Juan, xiii. 89.
A chessboard is essentially a square plane divided into sixty-four smaller
squares by straight lines at right angles. Originally it was not chequered (that
is, made with its rows and columns alternately black and white, or of any other
two colours), and this improvement was introduced merely to help the eye in
actual play. The utility of the chequers is unquestionable. For example, it
facilitates the operation of the bishops, enabling us to see at the merest
glance that our king or pawns on black squares are not open to attack from an
opponent's bishop running on the white diagonals. Yet the chequering of the
board is not essential to the game of chess. Also, when we are propounding
puzzles on the chessboard, it is often well to remember that additional interest
may result from "generalizing" for boards containing any number of squares, or
from limiting ourselves to some particular chequered arrangement, not
necessarily a square. We will give a few puzzles dealing with chequered boards
in this general way.
288.—CHEQUERED
BOARD DIVISIONS.
I recently asked myself the question: In how many different ways may a
chessboard be divided into two parts of the same size and shape by cuts along
the lines dividing the squares? The problem soon proved to be both fascinating
and bristling with difficulties. I present it in a simplified form, taking a
board of smaller dimensions.
It is obvious that a board of four squares can only be so divided in one
way—by a straight cut down the centre—because we shall not count reversals and
reflections as different. In the case of a board of sixteen squares—four by
four—there are just six different ways. I have given all these in the diagram,
and the reader will not find any others. Now, take the larger board of
thirty-six squares, and try to discover in how many ways it may be cut into two
parts of the same size and shape.
Solution 289.—LIONS
AND CROWNS.
The young lady in the illustration is confronted with a little cutting-out
difficulty in which the reader may be glad to assist her. She wishes, for some
reason that she has not communicated to me, to cut that square piece of valuable
material into four parts, all of exactly the same size and shape, but it is
important that every piece shall contain a lion and a crown. As she insists that
the cuts can only be made along the lines dividing the squares, she is
considerably perplexed to find out how it is to be done. Can you show her the
way? There is only one possible method of cutting the stuff.
Solution 290.—BOARDS
WITH AN ODD NUMBER OF SQUARES.
We will here consider the question of those boards that contain an odd number
of squares. We will suppose that the central square is first cut out, so as to
leave an even number of squares for division. Now, it is obvious that a square
three by three can only be divided in one way, as shown in Fig. 1. It will be
seen that the pieces A and B are of the same size and shape, and that any other
way of cutting would only produce the same shaped pieces, so remember that these
variations are not counted as different ways. The puzzle I propose is to cut the
board five by five (Fig. 2) into two pieces of the same size and shape in as
many different ways as possible. I have shown in the illustration one way of
doing it. How many different ways are there altogether? A piece which when
turned over resembles another piece is not considered to be of a different
shape.
Solution 291.—THE
GRAND LAMA'S PROBLEM.
Once upon a time there was a Grand Lama who had a chessboard made of pure
gold, magnificently engraved, and, of course, of great value. Every year a
tournament was held at Lhassa among the priests, and whenever any one beat the
Grand Lama it was considered a great honour, and his name was inscribed on the
back of the board, and a costly jewel set in the particular square on which the
checkmate had been given. After this sovereign pontiff had been defeated on four
occasions he died—possibly of chagrin.
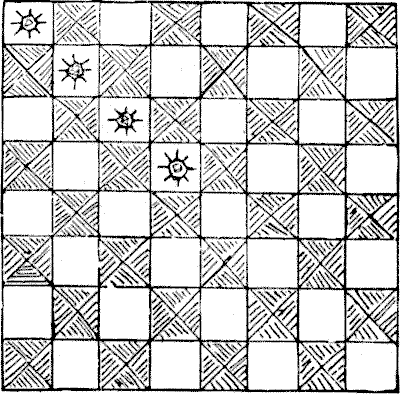
Now the new Grand Lama was an inferior chess-player, and preferred other
forms of innocent amusement, such as cutting off people's heads. So he
discouraged chess as a degrading game, that did not improve either the mind or
the morals, and abolished the tournament summarily. Then he sent for the four
priests who had had the effrontery to play better than a Grand Lama, and
addressed them as follows: "Miserable and heathenish men, calling yourselves
priests! Know ye not that to lay claim to a capacity to do anything better than
my predecessor is a capital offence? Take that chessboard and, before day dawns
upon the torture chamber, cut it into four equal parts of the same shape, each
containing sixteen perfect squares, with one of the gems in each part! If in
this you fail, then shall other sports be devised for your special delectation.
Go!" The four priests succeeded in their apparently hopeless task. Can you show
how the board may be divided into four equal parts, each of exactly the same
shape, by cuts along the lines dividing the squares, each part to contain one of
the gems?
Solution 292.—THE
ABBOT'S WINDOW.
Once upon a time the Lord Abbot of St. Edmondsbury, in consequence of
"devotions too strong for his head," fell sick and was unable to leave his bed.
As he lay awake, tossing his head restlessly from side to side, the attentive
monks noticed that something was disturbing his mind; but nobody dared ask what
it might be, for the abbot was of a stern disposition, and never would brook
inquisitiveness. Suddenly he called for Father John, and that venerable monk was
soon at the bedside.
"Father John," said the Abbot, "dost thou know that I came into this wicked
world on a Christmas Even?"
The monk nodded assent.
"And have I not often told thee that, having been born on Christmas Even, I
have no love for the things that are odd? Look there!"
The Abbot pointed to the large dormitory window, of which I give a sketch.
The monk looked, and was perplexed.
"Dost thou not see that the sixty-four lights add up an even number
vertically and horizontally, but that all the diagonal lines, except
fourteen are of a number that is odd? Why is this?"
"Of a truth, my Lord Abbot, it is of the very nature of things, and cannot be
changed."
"Nay, but it shall be changed. I command thee that certain of the
lights be closed this day, so that every line shall have an even number of
lights. See thou that this be done without delay, lest the cellars be locked up
for a month and other grievous troubles befall thee."
Father John was at his wits' end, but after consultation with one who was
learned in strange mysteries, a way was found to satisfy the whim of the Lord
Abbot. Which lights were blocked up, so that those which remained added up an
even number in every line horizontally, vertically, and diagonally, while the
least possible obstruction of light was caused?
Solution 293.—THE
CHINESE CHESSBOARD.
Into how large a number of different pieces may the chessboard be cut (by
cuts along the lines only), no two pieces being exactly alike? Remember that the
arrangement of black and white constitutes a difference. Thus, a single black
square will be different from a single white square, a row of three containing
two white squares will differ from a row of three containing two black, and so
on. If two pieces cannot be placed on the table so as to be exactly alike, they
count as different. And as the back of the board is plain, the pieces cannot be
turned over.
Solution 294.—THE
CHESSBOARD SENTENCE.
I once set myself the amusing task of so dissecting an ordinary chessboard
into letters of the alphabet that they would form a complete sentence. It will
be seen from the illustration that the pieces assembled give the sentence, "CUT
THY LIFE," with the stops between. The ideal sentence would, of course, have
only one full stop, but that I did not succeed in obtaining.
The sentence is an appeal to the transgressor to cut himself adrift from the
evil life he is living. Can you fit these pieces together to form a perfect
chessboard?
Solution
Previous Next
|