|
STATICAL
CHESS PUZZLES.
"They also serve who only stand and wait."
MILTON.
295.—THE
EIGHT ROOKS.
It will be seen in the first diagram that every square on the board is either
occupied or attacked by a rook, and that every rook is "guarded" (if they were
alternately black and white rooks we should say "attacked") by another rook.
Placing the eight rooks on any row or file obviously will have the same effect.
In diagram 2 every square is again either occupied or attacked, but in this case
every rook is unguarded. Now, in how many different ways can you so place the
eight rooks on the board that every square shall be occupied or attacked and no
rook ever guarded by another? I do not wish to go into the question of reversals
and reflections on this occasion, so that placing the rooks on the other
diagonal will count as different, and similarly with other repetitions obtained
by turning the board round.
Solution 296.—THE
FOUR LIONS.
The puzzle is to find in how many different ways the four lions may be placed
so that there shall never be more than one lion in any row or column. Mere
reversals and reflections will not count as different. Thus, regarding the
example given, if we place the lions in the other diagonal, it will be
considered the same arrangement. For if you hold the second arrangement in front
of a mirror or give it a quarter turn, you merely get the first arrangement. It
is a simple little puzzle, but requires a certain amount of careful
consideration.
Solution 297.—BISHOPS—UNGUARDED.
Place as few bishops as possible on an ordinary chessboard so that every
square of the board shall be either occupied or attacked. It will be seen that
the rook has more scope than the bishop: for wherever you place the former, it
will always attack fourteen other squares; whereas the latter will attack seven,
nine, eleven, or thirteen squares, according to the position of the diagonal on
which it is placed. And it is well here to state that when we speak of
"diagonals" in connection with the chessboard, we do not limit ourselves to the
two long diagonals from corner to corner, but include all the shorter lines that
are parallel to these. To prevent misunderstanding on future occasions, it will
be well for the reader to note carefully this fact.
Solution 298.—BISHOPS—GUARDED.
Now, how many bishops are necessary in order that every square shall be
either occupied or attacked, and every bishop guarded by another bishop? And how
may they be placed?
Solution 299.—BISHOPS
IN CONVOCATION.
The greatest number of bishops that can be placed at the same time on the
chessboard, without any bishop attacking another, is fourteen. I show, in
diagram, the simplest way of doing this. In fact, on a square chequered board of
any number of squares the greatest number of bishops that can be placed without
attack is always two less than twice the number of squares on the side. It is an
interesting puzzle to discover in just how many different ways the fourteen
bishops may be so placed without mutual attack. I shall give an exceedingly
simple rule for determining the number of ways for a square chequered board of
any number of squares.
Solution 300.—THE
EIGHT QUEENS.
The queen is by far the strongest piece on the chessboard. If you place her
on one of the four squares in the centre of the board, she attacks no fewer than
twenty-seven other squares; and if you try to hide her in a corner, she still
attacks twenty-one squares. Eight queens may be placed on the board so that no
queen attacks another, and it is an old puzzle (first proposed by Nauck in 1850,
and it has quite a little literature of its own) to discover in just how many
different ways this may be done. I show one way in the diagram, and there are in
all twelve of these fundamentally different ways. These twelve produce
ninety-two ways if we regard reversals and reflections as different. The diagram
is in a way a symmetrical arrangement. If you turn the page upside down, it will
reproduce itself exactly; but if you look at it with one of the other sides at
the bottom, you get another way that is not identical. Then if you reflect these
two ways in a mirror you get two more ways. Now, all the other eleven solutions
are non-symmetrical, and therefore each of them may be presented in eight ways
by these reversals and reflections. It will thus be seen why the twelve
fundamentally different solutions produce only ninety-two arrangements, as I
have said, and not ninety-six, as would happen if all twelve were
non-symmetrical. It is well to have a clear understanding on the matter of
reversals and reflections when dealing with puzzles on the chessboard.

Can the reader place the eight queens on the board so that no queen shall
attack another and so that no three queens shall be in a straight line in any
oblique direction? Another glance at the diagram will show that this arrangement
will not answer the conditions, for in the two directions indicated by the
dotted lines there are three queens in a straight line. There is only one of the
twelve fundamental ways that will solve the puzzle. Can you find it?
Solution 301.—THE
EIGHT STARS.
The puzzle in this case is to place eight stars in the diagram so that no
star shall be in line with another star horizontally, vertically, or diagonally.
One star is already placed, and that must not be moved, so there are only seven
for the reader now to place. But you must not place a star on any one of the
shaded squares. There is only one way of solving this little puzzle.
Solution 302.—A
PROBLEM IN MOSAICS.
The art of producing pictures or designs by means of joining together pieces
of hard substances, either naturally or artificially coloured, is of very great
antiquity. It was certainly known in the time of the Pharaohs, and we find a
reference in the Book of Esther to "a pavement of red, and blue, and white, and
black marble." Some of this ancient work that has come down to us, especially
some of the Roman mosaics, would seem to show clearly, even where design is not
at first evident, that much thought was bestowed upon apparently disorderly
arrangements. Where, for example, the work has been produced with a very limited
number of colours, there are evidences of great ingenuity in preventing the same
tints coming in close proximity. Lady readers who are familiar with the
construction of patchwork quilts will know how desirable it is sometimes, when
they are limited in the choice of material, to prevent pieces of the same stuff
coming too near together. Now, this puzzle will apply equally to patchwork
quilts or tesselated pavements.
It will be seen from the diagram how a square piece of flooring may be paved
with sixty-two square tiles of the eight colours violet, red, yellow, green,
orange, purple, white, and blue (indicated by the initial letters), so that no
tile is in line with a similarly coloured tile, vertically, horizontally, or
diagonally. Sixty-four such tiles could not possibly be placed under these
conditions, but the two shaded squares happen to be occupied by iron
ventilators.
The puzzle is this. These two ventilators have to be removed to the positions
indicated by the darkly bordered tiles, and two tiles placed in those bottom
corner squares. Can you readjust the thirty-two tiles so that no two of the same
colour shall still be in line?
Solution 303.—UNDER
THE VEIL.
If the reader will examine the above diagram, he will see that I have so
placed eight V's, eight E's, eight I's, and eight L's in the diagram that no
letter is in line with a similar one horizontally, vertically, or diagonally.
Thus, no V is in line with another V, no E with another E, and so on. There are
a great many different ways of arranging the letters under this condition. The
puzzle is to find an arrangement that produces the greatest possible number of
four-letter words, reading upwards and downwards, backwards and forwards, or
diagonally. All repetitions count as different words, and the five variations
that may be used are: VEIL, VILE, LEVI, LIVE, and EVIL.
This will be made perfectly clear when I say that the above arrangement
scores eight, because the top and bottom row both give VEIL; the second and
seventh columns both give VEIL; and the two diagonals, starting from the L in
the 5th row and E in the 8th row, both give LIVE and EVIL. There are therefore
eight different readings of the words in all.
This difficult word puzzle is given as an example of the use of chessboard
analysis in solving such things. Only a person who is familiar with the "Eight
Queens" problem could hope to solve it.
Solution 304.—BACHET'S
SQUARE.
One of the oldest card puzzles is by Claude Caspar Bachet de Méziriac, first
published, I believe, in the 1624 edition of his work. Rearrange the sixteen
court cards (including the aces) in a square so that in no row of four cards,
horizontal, vertical, or diagonal, shall be found two cards of the same suit or
the same value. This in itself is easy enough, but a point of the puzzle is to
find in how many different ways this may be done. The eminent French
mathematician A. Labosne, in his modern edition of Bachet, gives the answer
incorrectly. And yet the puzzle is really quite easy. Any arrangement produces
seven more by turning the square round and reflecting it in a mirror. These are
counted as different by Bachet.
Note "row of
four cards," so that the only diagonals we have here to consider are the two
long ones.
Solution 305.—THE
THIRTY-SIX LETTER BLOCKS.
The illustration represents a box containing thirty-six letter-blocks. The
puzzle is to rearrange these blocks so that no A shall be in a line vertically,
horizontally, or diagonally with another A, no B with another B, no C with
another C, and so on. You will find it impossible to get all the letters into
the box under these conditions, but the point is to place as many as possible.
Of course no letters other than those shown may be used.
Solution 306.—THE
CROWDED CHESSBOARD.
The puzzle is to rearrange the fifty-one pieces on the chessboard so that no
queen shall attack another queen, no rook attack another rook, no bishop attack
another bishop, and no knight attack another knight. No notice is to be taken of
the intervention of pieces of another type from that under consideration—that
is, two queens will be considered to attack one another although there may be,
say, a rook, a bishop, and a knight between them. And so with the rooks and
bishops. It is not difficult to dispose of each type of piece separately; the
difficulty comes in when you have to find room for all the arrangements on the
board simultaneously.
Solution 307.—THE
COLOURED COUNTERS.
The diagram represents twenty-five coloured counters, Red, Blue, Yellow,
Orange, and Green (indicated by their initials), and there are five of each
colour, numbered 1, 2, 3, 4, and 5. The problem is so to place them in a square
that neither colour nor number shall be found repeated in any one of the five
rows, five columns, and two diagonals. Can you so rearrange them?
Solution 308.—THE
GENTLE ART OF STAMP-LICKING.
The Insurance Act is a most prolific source of entertaining puzzles,
particularly entertaining if you happen to be among the exempt. One's initiation
into the gentle art of stamp-licking suggests the following little poser: If you
have a card divided into sixteen spaces (4 × 4), and are provided with
plenty of stamps of the values 1d., 2d., 3d., 4d.,
and 5d., what is the greatest value that you can stick on the card if the
Chancellor of the Exchequer forbids you to place any stamp in a straight line
(that is, horizontally, vertically, or diagonally) with another stamp of similar
value? Of course, only one stamp can be affixed in a space. The reader will
probably find, when he sees the solution, that, like the stamps themselves, he
is licked He will
most likely be twopence short of the maximum. A friend asked the Post Office how
it was to be done; but they sent him to the Customs and Excise officer, who sent
him to the Insurance Commissioners, who sent him to an approved society, who
profanely sent him—but no matter.
Solution 309.—THE
FORTY-NINE COUNTERS.
Can you rearrange the above forty-nine counters in a square so that no
letter, and also no number, shall be in line with a similar one, vertically,
horizontally, or diagonally? Here I, of course, mean in the lines parallel with
the diagonals, in the chessboard sense.
Solution 310.—THE
THREE SHEEP.
A farmer had three sheep and an arrangement of sixteen pens, divided off by
hurdles in the manner indicated in the illustration. In how many different ways
could he place those sheep, each in a separate pen, so that every pen should be
either occupied or in line (horizontally, vertically, or diagonally) with at
least one sheep? I have given one arrangement that fulfils the conditions. How
many others can you find? Mere reversals and reflections must not be counted as
different. The reader may regard the sheep as queens. The problem is then to
place the three queens so that every square shall be either occupied or attacked
by at least one queen—in the maximum number of different ways.
Solution 311.—THE
FIVE DOGS PUZZLE.
In 1863, C.F. de Jaenisch first discussed the "Five Queens Puzzle"—to place
five queens on the chessboard so that every square shall be attacked or
occupied—which was propounded by his friend, a "Mr. de R." Jaenisch showed that
if no queen may attack another there are ninety-one different ways of placing
the five queens, reversals and reflections not counting as different. If the
queens may attack one another, I have recorded hundreds of ways, but it is not
practicable to enumerate them exactly.
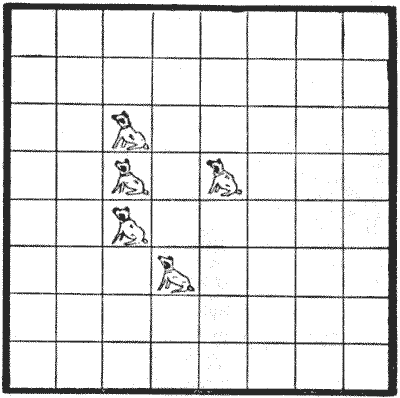
The illustration is supposed to represent an arrangement of sixty-four
kennels. It will be seen that five kennels each contain a dog, and on further
examination it will be seen that every one of the sixty-four kennels is in a
straight line with at least one dog—either horizontally, vertically, or
diagonally. Take any kennel you like, and you will find that you can draw a
straight line to a dog in one or other of the three ways mentioned. The puzzle
is to replace the five dogs and discover in just how many different ways they
may be placed in five kennels in a straight row, so that every kennel
shall always be in line with at least one dog. Reversals and reflections are
here counted as different.
Solution 312.—THE
FIVE CRESCENTS OF BYZANTIUM.
When Philip of Macedon, the father of Alexander the Great, found himself
confronted with great difficulties in the siege of Byzantium, he set his men to
undermine the walls. His desires, however, miscarried, for no sooner had the
operations been begun than a crescent moon suddenly appeared in the heavens and
discovered his plans to his adversaries. The Byzantines were naturally elated,
and in order to show their gratitude they erected a statue to Diana, and the
crescent became thenceforward a symbol of the state. In the temple that
contained the statue was a square pavement composed of sixty-four large and
costly tiles. These were all plain, with the exception of five, which bore the
symbol of the crescent. These five were for occult reasons so placed that every
tile should be watched over by (that is, in a straight line, vertically,
horizontally, or diagonally with) at least one of the crescents. The arrangement
adopted by the Byzantine architect was as follows:—

Now, to cover up one of these five crescents was a capital offence, the death
being something very painful and lingering. But on a certain occasion of
festivity it was necessary to lay down on this pavement a square carpet of the
largest dimensions possible, and I have shown in the illustration by dark
shading the largest dimensions that would be available.
The puzzle is to show how the architect, if he had foreseen this question of
the carpet, might have so arranged his five crescent tiles in accordance with
the required conditions, and yet have allowed for the largest possible square
carpet to be laid down without any one of the five crescent tiles being covered,
or any portion of them.
Solution 313.—QUEENS
AND BISHOP PUZZLE.
It will be seen that every square of the board is either occupied or
attacked. The puzzle is to substitute a bishop for the rook on the same square,
and then place the four queens on other squares so that every square shall again
be either occupied or attacked.
Solution 314.—THE
SOUTHERN CROSS.
In the above illustration we have five Planets and eighty-one Fixed Stars,
five of the latter being hidden by the Planets. It will be found that every
Star, with the exception of the ten that have a black spot in their centres, is
in a straight line, vertically, horizontally, or diagonally, with at least one
of the Planets. The puzzle is so to rearrange the Planets that all the Stars
shall be in line with one or more of them.
In rearranging the Planets, each of the five may be moved once in a straight
line, in either of the three directions mentioned. They will, of course, obscure
five other Stars in place of those at present covered.
Solution 315.—THE
HAT-PEG PUZZLE.
Here is a five-queen puzzle that I gave in a fanciful dress in 1897. As the
queens were there
represented as hats on sixty-four pegs, I will keep to the title, "The Hat-Peg
Puzzle." It will be seen that every square is occupied or attacked. The puzzle
is to remove one queen
to a different square so that still every square is occupied or attacked,
then move a second queen under a similar condition, then a third queen, and
finally a fourth queen. After the fourth move every square must be attacked or
occupied, but no queen must then attack another. Of course, the moves need not
be "queen moves;" you can move a queen to any part of the board.
Solution 316.—THE
AMAZONS.
This puzzle is based on one by Captain Turton. Remove three of the queens to
other squares so that there shall be eleven squares on the board that are not
attacked. The removal of the three queens need not be by "queen moves." You may
take them up and place them anywhere. There is only one solution.
Solution 317.—A
PUZZLE WITH PAWNS.
Place two pawns in the middle of the chessboard, one at Q 4 and the other at
K 5. Now, place the remaining fourteen pawns (sixteen in all) so that no three
shall be in a straight line in any possible direction.
Note that I purposely do not say queens, because by the words "any possible
direction" I go beyond attacks on diagonals. The pawns must be regarded as mere
points in space—at the centres of the squares. See dotted lines in the case of
No. 300,
"The
Eight Queens."
Solution 318.—LION-HUNTING.
My friend Captain Potham Hall, the renowned hunter of big game, says there is
nothing more exhilarating than a brush with a herd—a pack—a team—a flock—a swarm
(it has taken me a full quarter of an hour to recall the right word, but I have
it at last)—a pride of lions. Why a number of lions are called a "pride,"
a number of whales a "school," and a number of foxes a "skulk" are mysteries of
philology into which I will not enter.
Well, the captain says that if a spirited lion crosses your path in the
desert it becomes lively, for the lion has generally been looking for the man
just as much as the man has sought the king of the forest. And yet when they
meet they always quarrel and fight it out. A little contemplation of this
unfortunate and long-standing feud between two estimable families has led me to
figure out a few calculations as to the probability of the man and the lion
crossing one another's path in the jungle. In all these cases one has to start
on certain more or less arbitrary assumptions. That is why in the above
illustration I have thought it necessary to represent the paths in the desert
with such rigid regularity. Though the captain assures me that the tracks of the
lions usually run much in this way, I have doubts.
The puzzle is simply to find out in how many different ways the man and the
lion may be placed on two different spots that are not on the same path. By
"paths" it must be understood that I only refer to the ruled lines. Thus, with
the exception of the four corner spots, each combatant is always on two paths
and no more. It will be seen that there is a lot of scope for evading one
another in the desert, which is just what one has always understood.
Solution 319.—THE
KNIGHT-GUARDS.

The knight is the irresponsible low comedian of the chessboard. "He is a very
uncertain, sneaking, and demoralizing rascal," says an American writer. "He can
only move two squares, but makes up in the quality of his locomotion for its
quantity, for he can spring one square sideways and one forward simultaneously,
like a cat; can stand on one leg in the middle of the board and jump to any one
of eight squares he chooses; can get on one side of a fence and blackguard three
or four men on the other; has an objectionable way of inserting himself in safe
places where he can scare the king and compel him to move, and then gobble a
queen. For pure cussedness the knight has no equal, and when you chase him out
of one hole he skips into another." Attempts have been made over and over again
to obtain a short, simple, and exact definition of the move of the
knight—without success. It really consists in moving one square like a rook, and
then another square like a bishop—the two operations being done in one leap, so
that it does not matter whether the first square passed over is occupied by
another piece or not. It is, in fact, the only leaping move in chess. But
difficult as it is to define, a child can learn it by inspection in a few
minutes.
I have shown in the diagram how twelve knights (the fewest possible that will
perform the feat) may be placed on the chessboard so that every square is either
occupied or attacked by a knight. Examine every square in turn, and you will
find that this is so. Now, the puzzle in this case is to discover what is the
smallest possible number of knights that is required in order that every square
shall be either occupied or attacked, and every knight protected by another
knight. And how would you arrange them? It will be found that of the twelve
shown in the diagram only four are thus protected by being a knight's move from
another knight.
Solution
Previous Next
|