|
VARIOUS
ARITHMETICAL AND ALGEBRAICAL PROBLEMS.
"Variety's the very spice of
life,
That gives it all its
flavour."
COWPER: The
Task.
97.—THE
SPOT ON THE TABLE.
A boy, recently home from school, wished to give his father an exhibition of
his precocity. He pushed a large circular table into the corner of the room, as
shown in the illustration, so that it touched both walls, and he then pointed to
a spot of ink on the extreme edge.
"Here is a little puzzle for you, pater," said the youth. "That spot is
exactly eight inches from one wall and nine inches from the other. Can you tell
me the diameter of the table without measuring it?"
The boy was overheard to tell a friend, "It fairly beat the guv'nor;" but his father is
known to have remarked to a City acquaintance that he solved the thing in his
head in a minute. I often wonder which spoke the truth.
Solution
98.—ACADEMIC
COURTESIES.
In a certain mixed school, where a special feature was made of the
inculcation of good manners, they had a curious rule on assembling every
morning. There were twice as many girls as boys. Every girl made a bow to every
other girl, to every boy, and to the teacher. Every boy made a bow to every
other boy, to every girl, and to the teacher. In all there were nine hundred
bows made in that model academy every morning. Now, can you say exactly how many
boys there were in the school? If you are not very careful, you are likely to
get a good deal out in your calculation.
Solution
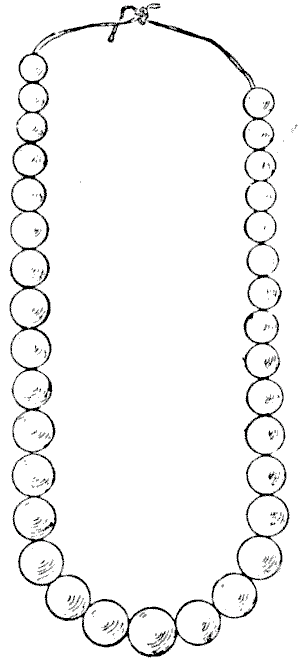
99.—THE
THIRTY-THREE PEARLS.
"A man I know," said Teddy Nicholson at a certain family party, "possesses a
string of thirty-three pearls. The middle pearl is the largest and best of all,
and the others are so selected and arranged that, starting from one end, each
successive pearl is worth £100 more than the preceding one, right up to the big
pearl. From the other end the pearls increase in value by £150 up to the large
pearl. The whole string is worth £65,000. What is the value of that large
pearl?"
"Pearls and other articles of clothing," said Uncle Walter, when the price of
the precious gem had been discovered, "remind me of Adam and Eve. Authorities,
you may not know, differ as to the number of apples that were eaten by Adam and
Eve. It is the opinion of some that Eve 8 (ate) and Adam 2 (too), a total of 10
only. But certain mathematicians have figured it out differently, and hold that
Eve 8 and Adam a total of 16. Yet the most recent investigators think the above
figures entirely wrong, for if Eve 8 and Adam 8 2, the total must be 90."
"Well," said Harry, "it seems to me that if there were giants in those days,
probably Eve 8 1 and Adam 8 2, which would give a total of 163."
"I am not at all satisfied," said Maud. "It seems to me that if Eve 8 1 and
Adam 8 1 2, they together consumed 893."
"I am sure you are all wrong," insisted Mr. Wilson, "for I consider that Eve
8 1 4 Adam, and Adam 8 1 2 4 Eve, so we get a total of 8,938."
"But, look here," broke in Herbert. "If Eve 8 1 4 Adam and Adam 8 1 2 4 2
oblige Eve, surely the total must have been 82,056!"
At this point Uncle Walter suggested that they might let the matter rest. He
declared it to be clearly what mathematicians call an indeterminate problem.
Solution
100.—THE
LABOURER'S PUZZLE.
Professor Rackbrane, during one of his rambles, chanced to come upon a man
digging a deep hole.
"Good morning," he said. "How deep is that hole?"
"Guess," replied the labourer. "My height is exactly five feet ten
inches."
"How much deeper are you going?" said the professor.
"I am going twice as deep," was the answer, "and then my head will be twice
as far below ground as it is now above ground."
Rackbrane now asks if you could tell how deep that hole would be when
finished.
Solution
101.—THE
TRUSSES OF HAY.
Farmer Tompkins had five trusses of hay, which he told his man Hodge to weigh
before delivering them to a customer. The stupid fellow weighed them two at a
time in all possible ways, and informed his master that the weights in pounds
were 110, 112, 113, 114, 115, 116, 117, 118, 120, and 121. Now, how was Farmer
Tompkins to find out from these figures how much every one of the five trusses
weighed singly? The reader may at first think that he ought to be told "which
pair is which pair," or something of that sort, but it is quite unnecessary. Can
you give the five correct weights?
Solution
102.—MR.
GUBBINS IN A FOG.
Mr. Gubbins, a diligent man of business, was much inconvenienced by a London
fog. The electric light happened to be out of order and he had to manage as best
he could with two candles. His clerk assured him that though both were of the same
length one candle would burn for four hours and the other for five hours. After
he had been working some time he put the candles out as the fog had lifted, and
he then noticed that what remained of one candle was exactly four times the
length of what was left of the other.
When he got home that night Mr. Gubbins, who liked a good puzzle, said to
himself, "Of course it is possible to work out just how long those two candles
were burning to-day. I'll have a shot at it." But he soon found himself in a
worse fog than the atmospheric one. Could you have assisted him in his dilemma?
How long were the candles burning?
Solution
103.—PAINTING
THE LAMP-POSTS.
Tim Murphy and Pat Donovan were engaged by the local authorities to paint the
lamp-posts in a certain street. Tim, who was an early riser, arrived first on
the job, and had painted three on the south side when Pat turned up and pointed
out that Tim's contract was for the north side. So Tim started afresh on the
north side and Pat continued on the south. When Pat had finished his side he
went across the street and painted six posts for Tim, and then the job was
finished. As there was an equal number of lamp-posts on each side of the street,
the simple question is: Which man painted the more lamp-posts, and just how many
more?
Solution
104.—CATCHING
THE THIEF.
"Now, constable," said the defendant's counsel in cross-examination," you say
that the prisoner was exactly twenty-seven steps ahead of you when you started
to run after him?"
"Yes, sir."
"And you swear that he takes eight steps to your five?"
"That is so."
"Then I ask you, constable, as an intelligent man, to explain how you ever
caught him, if that is the case?"
"Well, you see, I have got a longer stride. In fact, two of my steps are
equal in length to five of the prisoner's. If you work it out, you will find
that the number of steps I required would bring me exactly to the spot where I
captured him."
Here the foreman of the jury asked for a few minutes to figure out the number
of steps the constable must have taken. Can you also say how many steps the
officer needed to catch the thief?
Solution
105.—THE
PARISH COUNCIL ELECTION.
Here is an easy problem for the novice. At the last election of the parish
council of Tittlebury-in-the-Marsh there were twenty-three candidates for nine
seats. Each voter was qualified to vote for nine of these candidates or for any
less number. One of the electors wants to know in just how many different ways
it was possible for him to vote.
Solution
106.—THE
MUDDLETOWN ELECTION.
At the last Parliamentary election at Muddletown 5,473 votes were polled. The
Liberal was elected by a majority of 18 over the Conservative, by 146 over the
Independent, and by 575 over the Socialist. Can you give a simple rule for
figuring out how many votes were polled for each candidate?
Solution
107.—THE
SUFFRAGISTS' MEETING.
At a recent secret meeting of Suffragists a serious difference of opinion
arose. This led to a split, and a certain number left the meeting. "I had half a
mind to go myself," said the chair-woman, "and if I had done so, two-thirds of
us would have retired." "True," said another member; "but if I had persuaded my
friends Mrs. Wild and Christine Armstrong to remain we should only have lost
half our number." Can you tell how many were present at the meeting at the
start?
Solution
108.—THE
LEAP-YEAR LADIES.
Last leap-year ladies lost no time in exercising the privilege of making
proposals of marriage. If the figures that reached me from an occult source are
correct, the following represents the state of affairs in this country.
A number of women proposed once each, of whom one-eighth were widows. In
consequence, a number of men were to be married of whom one-eleventh were
widowers. Of the proposals made to widowers, one-fifth were declined. All the
widows were accepted. Thirty-five forty-fourths of the widows married bachelors.
One thousand two hundred and twenty-one spinsters were declined by bachelors.
The number of spinsters accepted by bachelors was seven times the number of
widows accepted by bachelors. Those are all the particulars that I was able to
obtain. Now, how many women proposed?
Solution
109.—THE
GREAT SCRAMBLE.
After dinner, the five boys of a household happened to find a parcel of
sugar-plums. It was quite unexpected loot, and an exciting scramble ensued, the
full details of which I will recount with accuracy, as it forms an interesting
puzzle.
You see, Andrew managed to get possession of just two-thirds of the parcel of
sugar-plums. Bob at once grabbed three-eighths of these, and Charlie managed to
seize three-tenths also. Then young David dashed upon the scene, and captured
all that Andrew had left, except one-seventh, which Edgar artfully secured for
himself by a cunning trick. Now the fun began in real earnest, for Andrew and
Charlie jointly set upon Bob, who stumbled against the fender and dropped half
of all that he had, which were equally picked up by David and Edgar, who had
crawled under a table and were waiting. Next, Bob sprang on Charlie from a
chair, and upset all the latter's collection on to the floor. Of this prize
Andrew got just a quarter, Bob gathered up one-third, David got two-sevenths, while
Charlie and Edgar divided equally what was left of that stock.

They were just thinking the fray was over when David suddenly struck out in
two directions at once, upsetting three-quarters of what Bob and Andrew had last
acquired. The two latter, with the greatest difficulty, recovered five-eighths
of it in equal shares, but the three others each carried off one-fifth of the
same. Every sugar-plum was now accounted for, and they called a truce, and
divided equally amongst them the remainder of the parcel. What is the smallest
number of sugar-plums there could have been at the start, and what proportion
did each boy obtain?
Solution
110.—THE
ABBOT'S PUZZLE.
The first English puzzlist whose name has come down to us was a
Yorkshireman—no other than Alcuin, Abbot of Canterbury (A.D. 735-804). Here is a
little puzzle from his works, which is at least interesting on account of its
antiquity. "If 100 bushels of corn were distributed among 100 people in such a
manner that each man received three bushels, each woman two, and each child half
a bushel, how many men, women, and children were there?"
Now, there are six different correct answers, if we exclude a case where
there would be no women. But let us say that there were just five times as many
women as men, then what is the correct solution?
Solution
111.—REAPING
THE CORN.
A farmer had a square cornfield. The corn was all ripe for reaping, and, as
he was short of men, it was arranged that he and his son should share the work
between them. The farmer first cut one rod wide all round the square, thus
leaving a smaller square of standing corn in the middle of the field. "Now," he
said to his son, "I have cut my half of the field, and you can do your share."
The son was not quite satisfied as to the proposed division of labour, and as
the village schoolmaster happened to be passing, he appealed to that person to
decide the matter. He found the farmer was quite correct, provided there was no
dispute as to the size of the field, and on this point they were agreed. Can you
tell the area of the field, as that ingenious schoolmaster succeeded in
doing?
Solution
112.—A
PUZZLING LEGACY.
A man left a hundred acres of land to be divided among his three sons—Alfred,
Benjamin, and Charles—in the proportion of one-third, one-fourth, and one-fifth
respectively. But Charles died. How was the land to be divided fairly between
Alfred and Benjamin?
Solution
113.—THE
TORN NUMBER.
I had the other day in my possession a label bearing the number 3 0 2 5 in
large figures. This got accidentally torn in half, so that 3 0 was on one piece
and 2 5 on the other, as shown on the illustration. On looking at these pieces I
began to make a calculation, scarcely conscious of what I was doing, when I
discovered this little peculiarity. If we add the 3 and the 2 5 together and
square the sum we get as the result the complete original number on the label!
Thus, 30 added to 25 is 55, and 55 multiplied by 55 is 3025. Curious, is it not?
Now, the puzzle is to find another number, composed of four figures, all
different, which may be divided in the middle and produce the same result.
Solution
114.—CURIOUS
NUMBERS.
The number 48 has this peculiarity, that if you add 1 to it the result is a
square number (49, the square of 7), and if you add 1 to its half, you also get
a square number (25, the square of 5). Now, there is no limit to the numbers
that have this peculiarity, and it is an interesting puzzle to find three more
of them—the smallest possible numbers. What are they?
Solution
115.—A
PRINTER'S ERROR.
In a certain article a printer had to set up the figures
54 × 23, which, of course, means that the fourth
power of 5 (625) is to be multiplied by the cube of 2 (8), the product of which
is 5,000. But he printed 54 × 23 as 5 4 2 3,
which is not correct. Can you place four digits in the manner shown, so that it
will be equally correct if the printer sets it up aright or makes the same
blunder?
Solution
116.—THE
CONVERTED MISER.
Mr. Jasper Bullyon was one of the very few misers who have ever been
converted to a sense of their duty towards their less fortunate fellow-men. One
eventful night he counted out his accumulated wealth, and resolved to distribute
it amongst the deserving poor.
He found that if he gave away the same number of pounds every day in the
year, he could exactly spread it over a twelvemonth without there being anything
left over; but if he rested on the Sundays, and only gave away a fixed number of
pounds every weekday, there would be one sovereign left over on New Year's Eve.
Now, putting it at the lowest possible, what was the exact number of pounds that
he had to distribute?
Could any question be simpler? A sum of pounds divided by one number of days
leaves no remainder, but divided by another number of days leaves a sovereign
over. That is all; and yet, when you come to tackle this little question, you
will be surprised that it can become so puzzling.
Solution
117.—A
FENCE PROBLEM.
The practical usefulness of puzzles is a point that we are liable to
overlook. Yet, as a matter of fact, I have from time to time received quite a
large number of letters from individuals who have found that the mastering of
some little principle upon which a puzzle was built has proved of considerable
value to them in a most unexpected way. Indeed, it may be accepted as a good
maxim that a puzzle is of little real value unless, as well as being amusing and
perplexing, it conceals some instructive and possibly useful feature. It is,
however, very curious how these little bits of acquired knowledge dovetail into
the occasional requirements of everyday life, and equally curious to what
strange and mysterious uses some of our readers seem to apply them. What, for
example, can be the object of Mr. Wm. Oxley, who writes to me all the way from
Iowa, in wishing to ascertain the dimensions of a field that he proposes to
enclose, containing just as many acres as there shall be rails in the fence?

The man wishes to fence in a perfectly square field which is to contain just
as many acres as there are rails in the required fence. Each hurdle, or portion
of fence, is seven rails high, and two lengths would extend one pole (16½ ft.):
that is to say, there are fourteen rails to the pole, lineal measure. Now, what
must be the size of the field?
Solution
118.—CIRCLING
THE SQUARES.
The puzzle is to place a different number in each of the ten squares so that
the sum of the squares of any two adjacent numbers shall be equal to the sum of
the squares of the two numbers diametrically opposite to them. The four numbers
placed, as examples, must stand as they are. The square of 16 is 256, and the
square of 2 is 4. Add these together, and the result is 260. Also—the square of
14 is 196, and the square of 8 is 64. These together also make 260. Now, in
precisely the same way, B and C should be equal to G and H (the sum will not
necessarily be 260), A and K to F and E, H and I to C and D, and so on, with any
two adjoining squares in the circle.
All you have to do is to fill in the remaining six numbers. Fractions are not
allowed, and I shall show that no number need contain more than two figures.
Solution
119.—RACKBRANE'S
LITTLE LOSS.
Professor Rackbrane was spending an evening with his old friends, Mr. and
Mrs. Potts, and they engaged in some game (he does not say what game) of cards.
The professor lost the first game, which resulted in doubling the money that
both Mr. and Mrs. Potts had laid on the table. The second game was lost by Mrs.
Potts, which doubled the money then held by her husband and the professor.
Curiously enough, the third game was lost by Mr. Potts, and had the effect of doubling the
money then held by his wife and the professor. It was then found that each
person had exactly the same money, but the professor had lost five shillings in
the course of play. Now, the professor asks, what was the sum of money with
which he sat down at the table? Can you tell him?
Solution
120.—THE
FARMER AND HIS SHEEP.
Farmer Longmore had a curious aptitude for arithmetic, and was known in his
district as the "mathematical farmer." The new vicar was not aware of this fact
when, meeting his worthy parishioner one day in the lane, he asked him in the
course of a short conversation, "Now, how many sheep have you altogether?" He
was therefore rather surprised at Longmore's answer, which was as follows: "You
can divide my sheep into two different parts, so that the difference between the
two numbers is the same as the difference between their squares. Maybe, Mr.
Parson, you will like to work out the little sum for yourself."
Can the reader say just how many sheep the farmer had? Supposing he had
possessed only twenty sheep, and he divided them into the two parts 12 and 8.
Now, the difference between their squares, 144 and 64, is 80. So that will not
do, for 4 and 80 are certainly not the same. If you can find numbers that work
out correctly, you will know exactly how many sheep Farmer Longmore owned.
Solution
121.—HEADS
OR TAILS.
Crooks, an inveterate gambler, at Goodwood recently said to a friend, "I'll
bet you half the money in my pocket on the toss of a coin—heads I win, tails I
lose." The coin was tossed and the money handed over. He repeated the offer
again and again, each time betting half the money then in his possession. We are
not told how long the game went on, or how many times the coin was tossed, but
this we know, that the number of times that Crooks lost was exactly equal to the
number of times that he won. Now, did he gain or lose by this little
venture?
Solution
122.—THE
SEE-SAW PUZZLE.
Necessity is, indeed, the mother of invention. I was amused the other day in
watching a boy who wanted to play see-saw and, in his failure to find another
child to share the sport with him, had been driven back upon the ingenious
resort of tying a number of bricks to one end of the plank to balance his weight
at the other.
As a matter of fact, he just balanced against sixteen bricks, when these were
fixed to the short end of plank, but if he fixed them to the long end of plank
he only needed eleven as balance.
Now, what was that boy's weight, if a brick weighs equal to a three-quarter brick and
three-quarters of a pound?
Solution
123.—A
LEGAL DIFFICULTY.
"A client of mine," said a lawyer, "was on the point of death when his wife
was about to present him with a child. I drew up his will, in which he settled
two-thirds of his estate upon his son (if it should happen to be a boy) and
one-third on the mother. But if the child should be a girl, then two-thirds of
the estate should go to the mother and one-third to the daughter. As a matter of
fact, after his death twins were born—a boy and a girl. A very nice point then
arose. How was the estate to be equitably divided among the three in the closest
possible accordance with the spirit of the dead man's will?"
Solution
124.—A
QUESTION OF DEFINITION.
"My property is exactly a mile square," said one landowner to another.
"Curiously enough, mine is a square mile," was the reply.
"Then there is no difference?"
Is this last statement correct?
Solution
125.—THE
MINERS' HOLIDAY.
Seven coal-miners took a holiday at the seaside during a big strike. Six of
the party spent exactly half a sovereign each, but Bill Harris was more
extravagant. Bill spent three shillings more than the average of the party. What
was the actual amount of Bill's expenditure?
Solution
126.—SIMPLE
MULTIPLICATION.
If we number six cards 1, 2, 4, 5, 7, and 8, and arrange them on the table in
this order:—
1 4 2 8
5 7
We can demonstrate that in order to multiply by 3 all that is necessary is to
remove the 1 to the other end of the row, and the thing is done. The answer is
428571. Can you find a number that, when multiplied by 3 and divided by 2, the
answer will be the same as if we removed the first card (which in this case is
to be a 3) From the beginning of the row to the end?
Solution
127.—SIMPLE
DIVISION.
Sometimes a very simple question in elementary arithmetic will cause a good
deal of perplexity. For example, I want to divide the four numbers, 701, 1,059,
1,417, and 2,312, by the largest number possible that will leave the same
remainder in every case. How am I to set to work Of course, by a laborious
system of trial one can in time discover the answer, but there is quite a simple
method of doing it if you can only find it.
Solution
128.—A
PROBLEM IN SQUARES.
We possess three square boards. The surface of the first contains five square
feet more than the second, and the second contains five square feet more than
the third. Can you give exact measurements for the sides of the boards? If you
can solve this little puzzle, then try to find three squares in arithmetical
progression, with a common difference of 7 and also of 13.
Solution
129.—THE
BATTLE OF HASTINGS.
All historians know that there is a great deal of mystery and uncertainty
concerning the details of the ever-memorable battle on that fatal day, October
14, 1066. My puzzle deals with a curious passage in an ancient monkish chronicle
that may never receive the attention that it deserves, and if I am unable to
vouch for the authenticity of the document it will none the less serve to
furnish us with a problem that can hardly fail to interest those of my readers
who have arithmetical predilections. Here is the passage in question.
"The men of Harold stood well together, as their wont was, and formed sixty
and one squares, with a like number of men in every square thereof, and woe to
the hardy Norman who ventured to enter their redoubts; for a single blow of a
Saxon war-hatchet would break his lance and cut through his coat of mail....
When Harold threw himself into the fray the Saxons were one mighty square of
men, shouting the battle-cries, 'Ut!' 'Olicrosse!' 'Godemitè!'"
Now, I find that all the contemporary authorities agree that the Saxons did
actually fight in this solid order. For example, in the "Carmen de Bello
Hastingensi," a poem attributed to Guy, Bishop of Amiens, living at the time of
the battle, we are told that "the Saxons stood fixed in a dense mass," and Henry
of Huntingdon records that "they were like unto a castle, impenetrable to the
Normans;" while Robert Wace, a century after, tells us the same thing. So in
this respect my newly-discovered chronicle may not be greatly in error. But I
have reason to believe that there is something wrong with the actual figures.
Let the reader see what he can make of them.
The number of men would be sixty-one times a square number; but when Harold
himself joined in the fray they were then able to form one large square. What is
the smallest possible number of men there could have been?
In order to make clear to the reader the simplicity of the question, I will
give the lowest solutions in the case of 60 and 62, the numbers immediately
preceding and following 61. They are 60 × 42 + 1
= 312, and
62 × 82 + 1 = 632. That is,
60 squares of 16 men each would be 960 men, and when Harold joined them they
would be 961 in number, and so form a square with 31 men on every side.
Similarly in the case of the figures I have given for 62. Now, find the lowest
answer for 61.
Solution
130.—THE
SCULPTOR'S PROBLEM.
An ancient sculptor was commissioned to supply two statues, each on a cubical
pedestal. It is with these pedestals that we are concerned. They were of unequal
sizes, as will be seen in the illustration, and when the time arrived for payment a dispute arose
as to whether the agreement was based on lineal or cubical measurement. But as
soon as they came to measure the two pedestals the matter was at once settled,
because, curiously enough, the number of lineal feet was exactly the same as the
number of cubical feet. The puzzle is to find the dimensions for two pedestals
having this peculiarity, in the smallest possible figures. You see, if the two
pedestals, for example, measure respectively 3 ft. and 1 ft. on every side, then
the lineal measurement would be 4 ft. and the cubical contents 28 ft., which are
not the same, so these measurements will not do.
Solution
131.—THE
SPANISH MISER.
There once lived in a small town in New Castile a noted miser named Don
Manuel Rodriguez. His love of money was only equalled by a strong passion for
arithmetical problems. These puzzles usually dealt in some way or other with his
accumulated treasure, and were propounded by him solely in order that he might
have the pleasure of solving them himself. Unfortunately very few of them have
survived, and when travelling through Spain, collecting material for a proposed
work on "The Spanish Onion as a Cause of National Decadence," I only discovered
a very few. One of these concerns the three boxes that appear in the
accompanying authentic portrait.

Each box contained a different number of golden doubloons. The difference
between the number of doubloons in the upper box and the number in the middle
box was the same as the difference between the number in the middle box and the
number in the bottom box. And if the contents of any two of the boxes were
united they would form a square number. What is the smallest number of doubloons
that there could have been in any one of the boxes?
Solution
132.—THE
NINE TREASURE BOXES.
The following puzzle will illustrate the importance on occasions of being
able to fix the minimum and maximum limits of a required number. This can very
frequently be done. For example, it has not yet been ascertained in how many
different ways the knight's tour can be performed on the chess board; but we
know that it is fewer than the number of combinations of 168 things taken 63 at
a time and is greater than 31,054,144—for the latter is the number of routes of
a particular type. Or, to take a more familiar case, if you ask a man how many
coins he has in his pocket, he may tell you that he has not the slightest idea.
But on further questioning you will get out of him some such statement as the
following: "Yes, I am positive that I have more than three coins, and equally
certain that there are not so many as twenty-five." Now, the knowledge that a
certain number lies between 2 and 12 in my puzzle will enable the solver to find
the exact answer; without that information there would be an infinite number of
answers, from which it would be impossible to select the correct one.
This is another puzzle received from my friend Don Manuel Rodriguez, the
cranky miser of New Castile. On New Year's Eve in 1879 he showed me nine
treasure boxes, and after informing me that every box contained a square number
of golden doubloons, and that the difference between the contents of A and B was
the same as between B and C, D and E, E and F, G and H, or H and I, he requested
me to tell him the number of coins in every one of the boxes. At first I thought
this was impossible, as there would be an infinite number of different answers,
but on consideration I found that this was not the case. I discovered that while
every box contained coins, the contents of A, B, C increased in weight in alphabetical order; so
did D, E, F; and so did G, H, I; but D or E need not be heavier than C, nor G or
H heavier than F. It was also perfectly certain that box A could not contain
more than a dozen coins at the outside; there might not be half that number, but
I was positive that there were not more than twelve. With this knowledge I was
able to arrive at the correct answer.
In short, we have to discover nine square numbers such that A, B, C; and D,
E, F; and G, H, I are three groups in arithmetical progression, the common
difference being the same in each group, and A being less than 12. How many
doubloons were there in every one of the nine boxes?
Solution
133.—THE
FIVE BRIGANDS.
The five Spanish brigands, Alfonso, Benito, Carlos, Diego, and Esteban, were
counting their spoils after a raid, when it was found that they had captured
altogether exactly 200 doubloons. One of the band pointed out that if Alfonso
had twelve times as much, Benito three times as much, Carlos the same amount,
Diego half as much, and Esteban one-third as much, they would still have
altogether just 200 doubloons. How many doubloons had each?
There are a good many equally correct answers to this question. Here is one
of them:
| A |
6 |
× |
12 |
= |
72 |
| B |
12 |
× |
3 |
= |
36 |
| C |
17 |
× |
1 |
= |
17 |
| D |
120 |
× |
½ |
= |
60 |
| E |
45 |
× |
1/3 |
= |
15 |
| |
200 |
|
|
|
200 |
The puzzle is to discover exactly how many different answers there are, it
being understood that every man had something and that there is to be no
fractional money—only doubloons in every case.
This problem, worded somewhat differently, was propounded by Tartaglia (died
1559), and he flattered himself that he had found one solution; but a French
mathematician of note (M.A. Labosne), in a recent work, says that his readers
will be astonished when he assures them that there are 6,639 different correct
answers to the question. Is this so? How many answers are there?
Solution
134.—THE
BANKER'S PUZZLE.
A banker had a sporting customer who was always anxious to wager on anything.
Hoping to cure him of his bad habit, he proposed as a wager that the customer
would not be able to divide up the contents of a box containing only sixpences
into an exact number of equal piles of sixpences. The banker was first to put in
one or more sixpences (as many as he liked); then the customer was to put in one
or more (but in his case not more than a pound in value), neither knowing what
the other put in. Lastly, the customer was to transfer from the banker's counter
to the box as many sixpences as the banker desired him to put in. The puzzle is
to find how many sixpences the banker should first put in and how many he should
ask the customer to transfer, so that he may have the best chance of
winning.
Solution
135.—THE
STONEMASON'S PROBLEM.
A stonemason once had a large number of cubic blocks of stone in his yard,
all of exactly the same size. He had some very fanciful little ways, and one of
his queer notions was to keep these blocks piled in cubical heaps, no two heaps
containing the same number of blocks. He had discovered for himself (a fact that
is well known to mathematicians) that if he took all the blocks contained in any
number of heaps in regular order, beginning with the single cube, he could
always arrange those on the ground so as to form a perfect square. This will be
clear to the reader, because one block is a square, 1 + 8 = 9 is a
square, 1 + 8 + 27 = 36 is a square,
1 + 8 + 27 + 64 = 100 is a square, and
so on. In fact, the sum of any number of consecutive cubes, beginning always
with 1, is in every case a square number.
One day a gentleman entered the mason's yard and offered him a certain price
if he would supply him with a consecutive number of these cubical heaps which
should contain altogether a number of blocks that could be laid out to form a
square, but the buyer insisted on more than three heaps and declined to take
the single block because it contained a flaw. What was the smallest possible
number of blocks of stone that the mason had to supply?
Solution
136.—THE
SULTAN'S ARMY.
A certain Sultan wished to send into battle an army that could be formed into
two perfect squares in twelve different ways. What is the smallest number of men
of which that army could be composed? To make it clear to the novice, I will
explain that if there were 130 men, they could be formed into two squares in
only two different ways—81 and 49, or 121 and 9. Of course, all the men must be
used on every occasion.
Solution
137.—A
STUDY IN THRIFT.
Certain numbers are called triangular, because if they are taken to represent
counters or coins they may be laid out on the table so as to form triangles. The
number 1 is always regarded as triangular, just as 1 is a square and a cube
number. Place one counter on the table—that is, the first triangular number. Now
place two more counters beneath it, and you have a triangle of three counters;
therefore 3 is triangular. Next place a row of three more counters, and you have
a triangle of six counters; therefore 6 is triangular. We see that every row of
counters that we add, containing just one more counter than the row above it,
makes a larger triangle.
Now, half the
sum of any number and its square is always a triangular number. Thus half of
2 + 22 = 3; half of
3 + 32 = 6; half of 4 +
42 = 10; half of 5 + 52= 15; and so
on. So if we want to form a triangle with 8 counters on each side we shall
require half of 8 + 82, or 36 counters. This is a pretty little
property of numbers. Before going further, I will here say that if the reader
refers to the "Stonemason's Problem" (No. 135) he will remember that the sum of
any number of consecutive cubes beginning with 1 is always a square, and these
form the series 12, 32, 62, 102,
etc. It will now be understood when I say that one of the keys to the puzzle was
the fact that these are always the squares of triangular numbers—that is, the
squares of 1, 3, 6, 10, 15, 21, 28, etc., any of which numbers we have seen will
form a triangle.
Every whole number is either triangular, or the sum of two triangular numbers
or the sum of three triangular numbers. That is, if we take any number we choose
we can always form one, two, or three triangles with them. The number 1 will
obviously, and uniquely, only form one triangle; some numbers will only form two
triangles (as 2, 4, 11, etc.); some numbers will only form three triangles (as
5, 8, 14, etc.). Then, again, some numbers will form both one and two triangles
(as 6), others both one and three triangles (as 3 and 10), others both two and
three triangles (as 7 and 9), while some numbers (like 21) will form one, two,
or three triangles, as we desire. Now for a little puzzle in triangular
numbers.
Sandy McAllister, of Aberdeen, practised strict domestic economy, and was
anxious to train his good wife in his own habits of thrift. He told her last New
Year's Eve that when she had saved so many sovereigns that she could lay them
all out on the table so as to form a perfect square, or a perfect triangle, or
two triangles, or three triangles, just as he might choose to ask he would add
five pounds to her treasure. Soon she went to her husband with a little bag of
£36 in sovereigns and claimed her reward. It will be found that the thirty-six
coins will form a square (with side 6), that they will form a single triangle
(with side 8), that they will form two triangles (with sides 5 and 6), and that
they will form three triangles (with sides 3, 5, and 5). In each of the four
cases all the thirty-six coins are used, as required, and Sandy therefore made
his wife the promised present like an honest man.
The Scotsman then undertook to extend his promise for five more years, so
that if next year the increased number of sovereigns that she has saved can be
laid out in the same four different ways she will receive a second present; if
she succeeds in the following year she will get a third present, and so on until
she has earned six presents in all. Now, how many sovereigns must she put
together before she can win the sixth present?
What you have to do is to find five numbers, the smallest possible, higher
than 36, that can be displayed in the four ways—to form a square, to form a
triangle, to form two triangles, and to form three triangles. The highest of
your five numbers will be your answer.
Solution
138.—THE
ARTILLERYMEN'S DILEMMA.
"All cannon-balls are to be piled in square pyramids," was the order issued
to the regiment. This was done. Then came the further order, "All pyramids are
to contain a square number of balls." Whereupon the trouble arose. "It can't be
done," said the major. "Look at this pyramid, for example; there are sixteen
balls at the base, then nine, then four, then one at the top, making thirty
balls in all. But there must be six more balls, or five fewer, to make a square
number." "It must be done," insisted the general. "All you have to do is
to put the right number of balls in your pyramids." "I've got it!" said a
lieutenant, the mathematical genius of the regiment. "Lay the balls out singly."
"Bosh!" exclaimed the general. "You can't pile one ball into a pyramid!"
Is it really possible to obey both orders?
Solution
139.—THE
DUTCHMEN'S WIVES.
I wonder how many of my readers are acquainted with the puzzle of the
"Dutchmen's Wives"—in which you have to determine the names of three men's
wives, or, rather, which wife belongs to each husband. Some thirty years ago it
was "going the rounds," as something quite new, but I recently discovered it in
the Ladies' Diary for 1739-40, so it was clearly familiar to the fair sex
over one hundred and seventy years ago. How many of our mothers, wives, sisters,
daughters, and aunts could solve the puzzle to-day? A far greater proportion
than then, let us hope.
Three Dutchmen, named Hendrick, Elas, and Cornelius, and their wives,
Gurtrün, Katrün, and Anna, purchase hogs. Each buys as many as he (or she) gives
shillings for one. Each husband pays altogether three guineas more than his
wife. Hendrick buys twenty-three more hogs than Katrün, and Elas eleven more
than Gurtrün.
Now, what was the name of each man's wife?
Solution
140.—FIND
ADA'S SURNAME.
This puzzle closely resembles the last one, my remarks on the solution of
which the reader may like to apply in another case. It was recently submitted to
a Sydney evening newspaper that indulges in "intellect sharpeners," but was
rejected with the remark that it is childish and that they only published
problems capable of solution! Five ladies, accompanied by their daughters,
bought cloth at the same shop. Each of the ten paid as many farthings per foot
as she bought feet, and each mother spent 8s. 5¼d. more than her
daughter. Mrs. Robinson spent 6s. more than Mrs. Evans, who spent about a
quarter as much as Mrs. Jones. Mrs. Smith spent most of all. Mrs. Brown bought
21 yards more than Bessie—one of the girls. Annie bought 16 yards more than Mary
and spent £3, 0s. 8d. more than Emily. The Christian name of the
other girl was Ada. Now, what was her surname?
Solution
141.—SATURDAY
MARKETING.
Here is an amusing little case of marketing which, although it deals with a
good many items of money, leads up to a question of a totally different
character. Four married couples went into their village on a recent Saturday
night to do a little marketing. They had to be very economical, for among them
they only possessed forty shilling coins. The fact is, Ann spent 1s.,
Mary spent 2s., Jane spent 3s., and Kate spent 4s. The men
were rather more extravagant than their wives, for Ned Smith spent as much as
his wife, Tom Brown twice as much as his wife, Bill Jones three times as much as
his wife, and Jack Robinson four times as much as his wife. On the way home
somebody suggested that they should divide what coin they had left equally among
them. This was done, and the puzzling question is simply this: What was the
surname of each woman? Can you pair off the four couples?
Solution
Previous Next
|