DYNAMICAL
CHESS PUZZLES.
"Push on—keep
moving."
THOS. MORTON: Cure for the
Heartache.
320.—THE
ROOK'S TOUR.
The puzzle is to move the single rook over the whole board, so that it shall
visit every square of the board once, and only once, and end its tour on the
square from which it starts. You have to do this in as few moves as possible,
and unless you are very careful you will take just one move too many. Of course,
a square is regarded equally as "visited" whether you merely pass over it or
make it a stopping-place, and we will not quibble over the point whether the
original square is actually visited twice. We will assume that it is not.
Solution 321.—THE
ROOK'S JOURNEY.
This puzzle I call "The Rook's Journey," because the word "tour" (derived
from a turner's wheel) implies that we return to the point from which we set
out, and we do not do this in the present case. We should not be satisfied with
a personally
conducted holiday tour that ended by leaving us, say, in the middle of the
Sahara. The rook here makes twenty-one moves, in the course of which journey it
visits every square of the board once and only once, stopping at the square
marked 10 at the end of its tenth move, and ending at the square marked 21. Two
consecutive moves cannot be made in the same direction—that is to say, you must
make a turn after every move.
Solution 322.—THE
LANGUISHING MAIDEN.
A wicked baron in the good old days imprisoned an innocent maiden in one of
the deepest dungeons beneath the castle moat. It will be seen from our
illustration that there were sixty-three cells in the dungeon, all connected by
open doors, and the maiden was chained in the cell in which she is shown. Now, a
valiant knight, who loved the damsel, succeeded in rescuing her from the enemy.
Having gained an entrance to the dungeon at the point where he is seen, he
succeeded in reaching the maiden after entering every cell once and only once.
Take your pencil and try to trace out such a route. When you have succeeded,
then try to discover a route in twenty-two straight paths through the cells. It
can be done in this number without entering any cell a second time.
Solution 323.—A
DUNGEON PUZZLE.
A French prisoner, for his sins (or other people's), was confined in an
underground dungeon containing sixty-four cells, all communicating with open
doorways, as shown in our illustration. In order to reduce the tedium of his
restricted life, he set himself various puzzles, and this is one of them.
Starting from the cell in which he is shown, how could he visit every cell once,
and only once, and make as many turnings as possible? His first attempt is shown
by the dotted track. It will be found that there are as many as fifty-five
straight lines in his path, but after many attempts he improved upon this. Can
you get more than fifty-five? You may end your path in any cell you like. Try
the puzzle with a pencil on chessboard diagrams, or you may regard them as
rooks' moves on a board.
Solution 324.—THE
LION AND THE MAN.
In a public place in Rome there once stood a prison divided into sixty-four
cells, all open to the sky and all communicating with one another, as shown in
the illustration. The sports that here took place were watched from a high
tower. The favourite game was to place a Christian in one corner cell and a lion
in the diagonally opposite corner and then leave them with all the inner doors
open. The consequent effect was sometimes most laughable. On one occasion the
man was given a sword. He was no coward, and was as anxious to find the lion as the
lion undoubtedly was to find him.
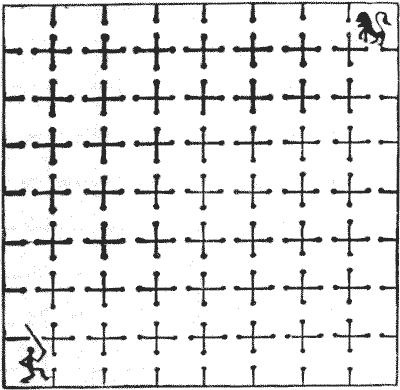
The man visited every cell once and only once in the fewest possible straight
lines until he reached the lion's cell. The lion, curiously enough, also visited
every cell once and only once in the fewest possible straight lines until he
finally reached the man's cell. They started together and went at the same
speed; yet, although they occasionally got glimpses of one another, they never
once met. The puzzle is to show the route that each happened to take.
Solution 325.—AN
EPISCOPAL VISITATION.
The white squares on the chessboard represent the parishes of a diocese.
Place the bishop on any square you like, and so contrive that (using the
ordinary bishop's move of chess) he shall visit every one of his parishes in the
fewest possible moves. Of course, all the parishes passed through on any move
are regarded as "visited." You can visit any squares more than once, but you are
not allowed to move twice between the same two adjoining squares. What are the
fewest possible moves? The bishop need not end his visitation at the parish from
which he first set out.
Solution 326.—A
NEW COUNTER PUZZLE.
Here is a new puzzle with moving counters, or coins, that at first glance
looks as if it must be absurdly simple. But it will be found quite a little
perplexity. I give it in this place for a reason that I will explain when we
come to the next puzzle. Copy the simple diagram, enlarged, on a sheet of paper;
then place two white counters on the points 1 and 2, and two red counters on 9
and 10, The puzzle is to make the red and white change places. You may move the
counters one at a time in any order you like, along the lines from point to
point, with the only restriction that a red and a white counter may never stand
at once on the same straight line. Thus the first move can only be from 1 or 2
to 3, or from 9 or 10 to 7.
Solution 327.—A
NEW BISHOP'S PUZZLE.
This is quite a fascinating little puzzle. Place eight bishops (four black
and four white) on the reduced chessboard, as shown in the illustration. The
problem is to make the black bishops change places with the white ones, no
bishop ever attacking another of the opposite colour. They must move
alternately—first a white, then a black, then a white, and so on. When you have
succeeded in doing it at all, try to find the fewest possible moves.
If you leave out the bishops standing on black squares, and only play on the
white squares, you will discover my last puzzle turned on its side.
Solution 328.—THE
QUEEN'S TOUR.
The puzzle of making a complete tour of the chessboard with the queen in the
fewest possible moves (in which squares may be visited more than once) was first
given by the late Sam Loyd in his Chess Strategy. But the solution shown
below is the one he gave in American Chess-Nuts in 1868. I have recorded
at least six different solutions in the minimum number of moves—fourteen—but
this one is the best of all, for reasons I will explain.

If you will look at the lettered square you will understand that there are
only ten really differently placed squares on a chessboard—those enclosed by a
dark line—all the others are mere reversals or reflections. For example, every A
is a corner square, and every J a central square. Consequently, as the solution
shown has a turning-point at the enclosed D square, we can obtain a solution
starting from and ending at any square marked D—by just turning the board about.
Now, this scheme will give you a tour starting from any A, B, C, D, E, F, or H,
while no other route that I know can be adapted to more than five different
starting-points. There is no Queen's Tour in fourteen moves (remember a tour
must be re-entrant) that may start from a G, I, or J. But we can have a
non-re-entrant path over the whole board in fourteen moves, starting from any
given square. Hence the following puzzle:—
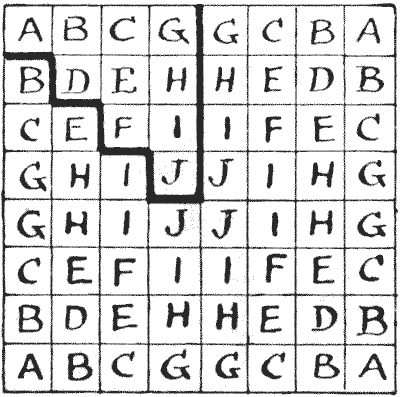
Start from the J in the enclosed part of the lettered diagram and visit every
square of the board in fourteen moves, ending wherever you like.
Solution 329.—THE
STAR PUZZLE.
Put the point of your pencil on one of the white stars and (without ever
lifting your pencil from the paper) strike out all the stars in fourteen
continuous straight strokes, ending at the second white star. Your straight
strokes may be in any direction you like, only every turning must be made on a
star. There is no objection to striking out any star more than once.
In this case, where both your starting and ending squares are fixed
inconveniently, you cannot obtain a solution by breaking a Queen's Tour, or in
any other way by queen moves alone. But you are allowed to use oblique straight
lines—such as from the upper white star direct to a corner star.
Solution 330.—THE
YACHT RACE.
Now then, ye land-lubbers, hoist your baby-jib-topsails, break out your
spinnakers, ease off your balloon sheets, and get your head-sails set!
Our race consists in starting from the point at which the yacht is lying in
the illustration and touching every one of the sixty-four buoys in fourteen
straight courses, returning in the final tack to the buoy from which we start.
The seventh course must finish at the buoy from which a flag is flying.
This puzzle will call for a lot of skilful seamanship on account of the sharp
angles at which it will occasionally be necessary to tack. The point of a lead
pencil and a good nautical eye are all the outfit that we require.
This is difficult, because of the condition as to the flag-buoy, and because
it is a re-entrant tour. But again we are allowed those oblique lines.
Solution 331.—THE
SCIENTIFIC SKATER.
It will be seen that this skater has marked on the ice sixty-four points or
stars, and he proposes to start from his present position near the corner
and enter every one of the points in fourteen straight lines. How will he do it?
Of course there is no objection to his passing over any point more than once,
but his last straight stroke must bring him back to the position from which he
started.
It is merely a matter of taking your pencil and starting from the spot on
which the skater's foot is at present resting, and striking out all the stars in
fourteen continuous straight lines, returning to the point from which you set
out.
Solution 332.—THE
FORTY-NINE STARS.
The puzzle in this case is simply to take your pencil and, starting from one
black star, strike out all the stars in twelve straight strokes, ending at the
other black star. It will be seen that the attempt shown in the illustration
requires fifteen strokes. Can you do it in twelve? Every turning must be made on
a star, and the lines must be parallel to the sides and diagonals of the square,
as shown. In this case we are dealing with a chessboard of reduced dimensions,
but only queen moves (without going outside the boundary as in the last case)
are required.
Solution 333.—THE
QUEEN'S JOURNEY.
Place the queen on her own square, as shown in the illustration, and then try
to discover the greatest distance that she can travel over the board in
five queen's moves without passing over any square a second time. Mark the
queen's path on the board, and note carefully also that she must never cross her
own track. It seems simple enough, but the reader may find that he has
tripped.
Solution 334.—ST.
GEORGE AND THE DRAGON.
Here is a little puzzle on a reduced chessboard of forty-nine squares. St.
George wishes to kill the dragon. Killing dragons was a well-known pastime of
his, and, being a knight, it was only natural that he should desire to perform
the feat in a series of knight's moves. Can you show how, starting from that
central square, he may visit once, and only once, every square of the board in a
chain of chess knight's moves, and end by capturing the dragon on his last move?
Of course a variety of different ways are open to him, so try to discover a
route that forms some pretty design when you have marked each successive leap by
a straight line from square to square.
Solution 335.—FARMER
LAWRENCE'S CORNFIELDS.
One of the most beautiful districts within easy distance of London for a
summer ramble is that part of Buckinghamshire known as the Valley of the
Chess—at least, it was a few years ago, before it was discovered by the
speculative builder. At the beginning of the present century there lived, not
far from Latimers, a worthy but eccentric farmer named Lawrence. One of his
queer notions was that every person who lived near the banks of the river Chess
ought to be in some way acquainted with the noble game of the same name, and in
order to impress this fact on his men and his neighbours he adopted at times
strange terminology. For example, when one of his ewes presented him with a
lamb, he would say that it had "queened a pawn"; when he put up a new barn
against the highway, he called it "castling on the king's side"; and when he
sent a man with a gun to keep his neighbour's birds off his fields, he spoke of
it as "attacking his opponent's rooks." Everybody in the neighbourhood used to
be amused at Farmer Lawrence's little jokes, and one boy (the wag of the
village) who got his ears pulled by the old gentleman for stealing his
"chestnuts" went so far as to call him "a silly old chess-protector!"
One year he had a large square field divided into forty-nine square plots, as
shown in the illustration. The white squares were sown with wheat and the black
squares with barley. When the harvest time came round he gave orders that his
men were first to cut the corn in the patch marked 1, and that each successive
cutting should be exactly a knight's move from the last one, the thirteenth
cutting being in the patch marked 13, the twenty-fifth in the patch marked 25,
the thirty-seventh in the one marked 37, and the last, or forty-ninth cutting,
in the patch marked 49. This was too much for poor Hodge, and each day Farmer
Lawrence had to go down to the field and show which piece had to be operated
upon. But the problem will perhaps present no difficulty to my readers.
Solution 336.—THE
GREYHOUND PUZZLE.
In this puzzle the twenty kennels do not communicate with one another by
doors, but are divided off by a low wall. The solitary occupant is the greyhound
which lives in the kennel in the top left-hand corner. When he is allowed his
liberty he has to obtain it by visiting every kennel once and only once in a
series of knight's moves, ending at the bottom right-hand corner, which is
open to the world. The lines in the above diagram show one solution. The puzzle
is to discover in how many different ways the greyhound may thus make his exit
from his corner kennel.
Solution 337.—THE
FOUR KANGAROOS.
In introducing a little Commonwealth problem, I must first explain that the
diagram represents the sixty-four fields, all properly fenced off from one
another, of an Australian settlement, though I need hardly say that our kith and
kin "down under" always do set out their land in this methodical and
exact manner. It will be seen that in every one of the four corners is a
kangaroo. Why kangaroos have a marked preference for corner plots has never been
satisfactorily explained, and it would be out of place to discuss the point
here. I should also add that kangaroos, as is well known, always leap in what we
call "knight's moves." In fact, chess players would probably have adopted the
better term "kangaroo's move" had not chess been invented before kangaroos.
The puzzle is simply this. One morning each kangaroo went for his morning
hop, and in sixteen consecutive knight's leaps visited just fifteen different
fields and jumped back to his corner. No field was visited by more than one of
the kangaroos. The diagram shows how they arranged matters. What you are asked
to do is to show how they might have performed the feat without any kangaroo
ever crossing the horizontal line in the middle of the square that divides the
board into two equal parts.
Solution 338.—THE
BOARD IN COMPARTMENTS.
We cannot divide the ordinary chessboard into four equal square compartments,
and describe a complete tour, or even path, in each compartment. But we may
divide it into four compartments, as in the illustration, two containing each
twenty squares, and the other two each twelve squares, and so obtain an
interesting puzzle. You are asked to describe a complete re-entrant tour on this
board, starting where you like, but visiting every square in each successive
compartment before passing into another one, and making the final leap back to
the square from which the knight set out. It is not difficult, but will be found
very entertaining and not uninstructive.
Whether a re-entrant "tour" or a complete knight's "path" is possible or not
on a rectangular board of given dimensions depends not only on its dimensions,
but also on its shape. A tour is obviously not possible on a board containing an
odd number of cells, such as 5 by 5 or 7 by 7, for this reason: Every successive
leap of the knight must be from a white square to a black and a black to a white
alternately. But if there be an odd number of cells or squares there must be one
more square of one colour than of the other, therefore the path must begin from
a square of the colour that is in excess, and end on a similar colour, and as a
knight's move
from one colour to a similar colour is impossible the path cannot be re-entrant.
But a perfect tour may be made on a rectangular board of any dimensions provided
the number of squares be even, and that the number of squares on one side be not
less than 6 and on the other not less than 5. In other words, the smallest
rectangular board on which a re-entrant tour is possible is one that is 6 by
5.
A complete knight's path (not re-entrant) over all the squares of a board is
never possible if there be only two squares on one side; nor is it possible on a
square board of smaller dimensions than 5 by 5. So that on a board 4 by 4 we can
neither describe a knight's tour nor a complete knight's path; we must leave one
square unvisited. Yet on a board 4 by 3 (containing four squares fewer) a
complete path may be described in sixteen different ways. It may interest the
reader to discover all these. Every path that starts from and ends at different
squares is here counted as a different solution, and even reverse routes are
called different.
Solution 339.—THE
FOUR KNIGHTS' TOURS.
I will repeat that if a chessboard be cut into four equal parts, as indicated
by the dark lines in the illustration, it is not possible to perform a knight's
tour, either re-entrant or not, on one of the parts. The best re-entrant attempt
is shown, in which each knight has to trespass twice on other parts. The puzzle
is to cut the board differently into four parts, each of the same size and
shape, so that a re-entrant knight's tour may be made on each part. Cuts along
the dotted lines will not do, as the four central squares of the board would be
either detached or hanging on by a mere thread.
Solution 340.—THE
CUBIC KNIGHT'S TOUR.
Some few years ago I happened to read somewhere that Abnit Vandermonde, a
clever mathematician, who was born in 1736 and died in 1793, had devoted a good
deal of study to the question of knight's tours. Beyond what may be gathered
from a few fragmentary references, I am not aware of the exact nature or results
of his investigations, but one thing attracted my attention, and that was the
statement that he had proposed the question of a tour of the knight over the six
surfaces of a cube, each surface being a chessboard. Whether he obtained a
solution or not I do not know, but I have never seen one published. So I at once
set to work to master this interesting problem. Perhaps the reader may like to
attempt it.
Solution 341.—THE
FOUR FROGS.
In the illustration we have eight toadstools, with white frogs on 1 and 3 and
black frogs on 6 and 8. The puzzle is to move one frog at a time, in any order,
along one of the straight lines from toadstool to toadstool, until they have
exchanged places, the white frogs being left on 6 and 8 and the black ones on 1
and 3. If you use four counters on a simple diagram, you will find this quite
easy, but it is a little more puzzling to do it in only seven plays, any number
of successive moves by one frog counting as one play. Of course, more than one
frog cannot be on a toadstool at the same time.
Solution 342.—THE
MANDARIN'S PUZZLE.
The following puzzle has an added interest from the circumstance that a
correct solution of it secured for a certain young Chinaman the hand of his
charming bride. The wealthiest mandarin within a radius of a hundred miles of
Peking was Hi-Chum-Chop, and his beautiful daughter, Peeky-Bo, had innumerable
admirers. One of her most ardent lovers was Winky-Hi, and when he asked the old
mandarin for his consent to their marriage, Hi-Chum-Chop presented him with the
following puzzle and promised his consent if the youth brought him the correct
answer within a week. Winky-Hi, following a habit which obtains among certain
solvers to
this day, gave it to all his friends, and when he had compared their solutions
he handed in the best one as his own. Luckily it was quite right. The mandarin
thereupon fulfilled his promise. The fatted pup was killed for the wedding
feast, and when Hi-Chum-Chop passed Winky-Hi the liver wing all present knew
that it was a token of eternal goodwill, in accordance with Chinese custom from
time immemorial.
The mandarin had a table divided into twenty-five squares, as shown in the
diagram. On each of twenty-four of these squares was placed a numbered counter,
just as I have indicated. The puzzle is to get the counters in numerical order
by moving them one at a time in what we call "knight's moves." Counter 1 should
be where 16 is, 2 where 11 is, 4 where 13 now is, and so on. It will be seen
that all the counters on shaded squares are in their proper positions. Of
course, two counters may never be on a square at the same time. Can you perform
the feat in the fewest possible moves?
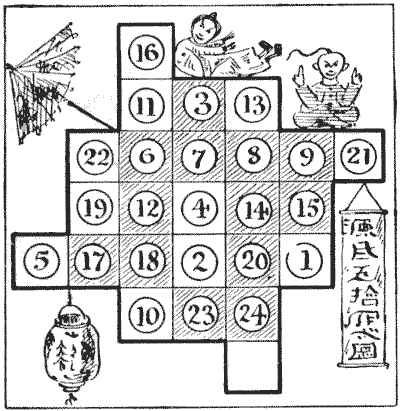
In order to make the manner of moving perfectly clear I will point out that
the first knight's move can only be made by 1 or by 2 or by 10. Supposing 1
moves, then the next move must be by 23, 4, 8, or 21. As there is never more
than one square vacant, the order in which the counters move may be written out
as follows: 1—21—14—18—22, etc. A rough diagram should be made on a larger scale
for practice, and numbered counters or pieces of cardboard used.
Solution 343.—EXERCISE
FOR PRISONERS.
The following is the plan of the north wing of a certain gaol, showing the
sixteen cells all communicating by open doorways. Fifteen prisoners were
numbered and arranged in the cells as shown. They were allowed to change their
cells as much as they liked, but if two prisoners were ever in the same cell
together there was a severe punishment promised them.
Now, in order to reduce their growing obesity, and to combine physical
exercise with mental recreation, the prisoners decided, on the suggestion of one
of their number who was interested in knight's tours, to try to form themselves
into a perfect knight's path without breaking the prison regulations, and
leaving the bottom right-hand corner cell vacant, as originally. The joke of the
matter is that the arrangement at which they arrived was as follows:—
| 8 |
3 |
12 |
1 |
| 11 |
14 |
9 |
6 |
| 4 |
7 |
2 |
13 |
| 15 |
10 |
5 |
The warders failed to detect the important fact that the men could not
possibly get into this position without two of them having been at some time in
the same cell together. Make the attempt with counters on a ruled diagram, and
you will find that this is so. Otherwise the solution is correct enough, each
member being, as required, a knight's move from the preceding number, and the
original corner cell vacant.
The puzzle is to start with the men placed as in the illustration and show
how it might have been done in the fewest moves, while giving a complete rest to
as many prisoners as possible.
As there is never more than one vacant cell for a man to enter, it is only
necessary to write down the numbers of the men in the order in which they move.
It is clear that very few men can be left throughout in their cells undisturbed,
but I will leave the solver to discover just how many, as this is a very
essential part of the puzzle.
Solution 344.—THE
KENNEL PUZZLE.
A man has twenty-five dog kennels all communicating with each other by
doorways, as shown in the illustration. He wishes to arrange his twenty dogs so
that they shall form a knight's string from dog No. 1 to dog No. 20, the bottom
row of five kennels to be left empty, as at present. This is to be done by
moving one dog at a time into a vacant kennel. The dogs are well trained to
obedience, and may be trusted to remain in the kennels in which they are placed,
except that if two are placed in the same kennel together they will fight it out
to the death. How is the puzzle to be solved in the fewest possible moves
without two dogs ever being together?
Solution 345.—THE
TWO PAWNS.
Here is a neat little puzzle in counting. In how many different ways may the
two pawns advance to the eighth square? You may move them in any order you like
to form a different sequence. For example, you may move the Q R P (one or two
squares) first, or the K R P first, or one pawn as far as you like before
touching the other. Any sequence is permissible, only in this puzzle as soon as
a pawn reaches the eighth square it is dead, and remains there unconverted. Can
you count the number of different sequences? At first it will strike you as
being very difficult, but I will show that it is really quite simple when
properly attacked.
Solution
Previous Next
|