|
MOVING
COUNTER PROBLEMS.
"I cannot do't without counters."
Winter's Tale, iv. 3.
Puzzles of this class, except so far as they occur in connection with actual
games, such as chess, seem to be a comparatively modern introduction.
Mathematicians in recent times, notably Vandermonde and Reiss, have devoted some
attention to them, but they do not appear to have been considered by the old
writers. So far as games with counters are concerned, perhaps the most ancient
and widely known in old times is "Nine Men's Morris" (known also, as I shall
show, under a great many other names), unless the simpler game, distinctly
mentioned in the works of Ovid (No. 110, "Ovid's Game," in The Canterbury
Puzzles), from which "Noughts and Crosses" seems to be derived, is still
more ancient.
In France the game is called Marelle, in Poland Siegen Wulf Myll (She-goat
Wolf Mill, or Fight), in Germany and Austria it is called Muhle (the Mill), in
Iceland it goes by the name of Mylla, while the Bogas (or native bargees) of
South America are said to play it, and on the Amazon it is called Trique, and
held to be of Indian origin. In our own country it has different names in
different districts, such as Meg Merrylegs, Peg Meryll, Nine Peg o'Merryal,
Nine-Pin Miracle, Merry Peg, and Merry Hole. Shakespeare refers to it in
"Midsummer Night's Dream" (Act ii., scene 1):—
"The nine-men's morris is filled up with
mud;
And the quaint mazes in the
wanton green,
For lack of tread, are
undistinguishable."
It was played by the shepherds with stones in holes cut in the turf. John
Clare, the peasant poet of Northamptonshire, in "The Shepherd Boy" (1835)
says:—"Oft we track his haunts .... By nine-peg-morris nicked upon the green."
It is also mentioned by Drayton in his "Polyolbion."
It was found on an old Roman tile discovered during the excavations at
Silchester, and cut upon the steps of the Acropolis at Athens. When visiting the
Christiania Museum a few years ago I was shown the great Viking ship that was
discovered at Gokstad in 1880. On the oak planks forming the deck of the vessel
were found boles and lines marking out the game, the holes being made to receive
pegs. While inspecting the ancient oak furniture in the Rijks Museum at
Amsterdam I became interested in an old catechumen's settle, and was surprised
to find the game diagram cut in the centre of the seat—quite conveniently for
surreptitious play. It has been discovered cut in the choir stalls of several of
our English cathedrals. In the early eighties it was found scratched upon a
stone built into a wall (probably about the date 1200), during the restoration
of Hargrave church in Northamptonshire. This stone is now in the Northampton
Museum. A similar stone has since been found at Sempringham, Lincolnshire. It is
to be seen on an ancient tombstone in the Isle of Man, and painted on old Dutch
tiles. And in 1901 a stone was dug out of a gravel pit near Oswestry bearing an
undoubted diagram of the game.
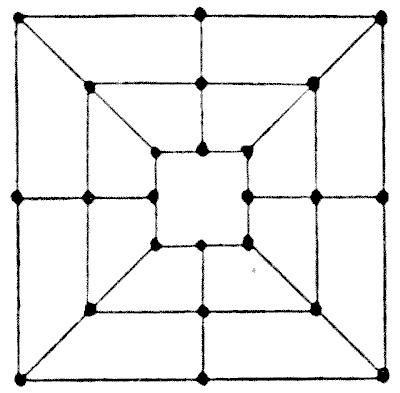
The game has been played with different rules at different periods and places. I give
a copy of the board. Sometimes the diagonal lines are omitted, but this
evidently was not intended to affect the play: it simply meant that the angles
alone were thought sufficient to indicate the points. This is how Strutt, in
Sports and Pastimes, describes the game, and it agrees with the way I
played it as a boy:—"Two persons, having each of them nine pieces, or men, lay
them down alternately, one by one, upon the spots; and the business of either
party is to prevent his antagonist from placing three of his pieces so as to
form a row of three, without the intervention of an opponent piece. If a row be
formed, he that made it is at liberty to take up one of his competitor's pieces
from any part he thinks most to his advantage; excepting he has made a row,
which must not be touched if he have another piece upon the board that is not a
component part of that row. When all the pieces are laid down, they are played
backwards and forwards, in any direction that the lines run, but only can move
from one spot to another (next to it) at one time. He that takes off all his
antagonist's pieces is the conqueror."
214.—THE
SIX FROGS.
The six educated frogs in the illustration are trained to reverse their
order, so that their numbers shall read 6, 5, 4, 3, 2, 1, with the blank square
in its present position. They can jump to the next square (if vacant) or leap
over one frog to the next square beyond (if vacant), just as we move in the game
of draughts, and can go backwards or forwards at pleasure. Can you show how they
perform their feat in the fewest possible moves? It is quite easy, so when you
have done it add a seventh frog to the right and try again. Then add more frogs
until you are able to give the shortest solution for any number. For it can
always be done, with that single vacant square, no matter how many frogs there
are.
Solution 215.—THE
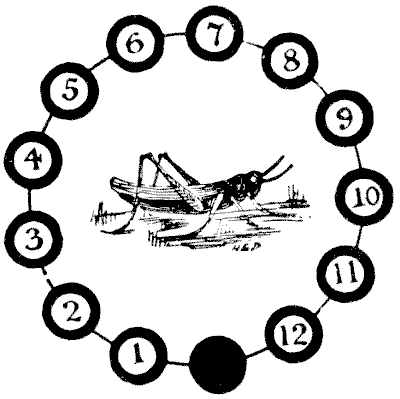
GRASSHOPPER PUZZLE.
It has been suggested that this puzzle was a great favourite among the young
apprentices of the City of London in the sixteenth and seventeenth centuries.
Readers will have noticed the curious brass grasshopper on the Royal Exchange.
This long-lived creature escaped the fires of 1666 and 1838. The grasshopper,
after his kind, was the crest of Sir Thomas Gresham, merchant grocer, who died
in 1579, and from this cause it has been used as a sign by grocers in general.
Unfortunately for the legend as to its origin, the puzzle was only produced by
myself so late as the year 1900. On twelve of the thirteen black discs are
placed numbered counters or grasshoppers. The puzzle is to reverse their order,
so that they shall read, 1, 2, 3, 4, etc., in the opposite direction, with the
vacant disc left in the same position as at present. Move one at a time in any
order, either to the adjoining vacant disc or by jumping over one grasshopper,
like the moves in draughts. The moves or leaps may be made in either direction
that is at any time possible. What are the fewest possible moves in which it can
be done?
Solution 216.—THE
EDUCATED FROGS.
Our six educated frogs have learnt a new and pretty feat. When placed on
glass tumblers, as shown in the illustration, they change sides so that the
three black ones are to the left and the white frogs to the right, with the
unoccupied tumbler at the opposite end—No. 7. They can jump to the next tumbler
(if unoccupied), or over one, or two, frogs to an unoccupied tumbler. The jumps
can be made in either direction, and a frog may jump over his own or the
opposite colour, or both colours. Four successive specimen jumps will make everything quite plain:
4 to 1, 5 to 4, 3 to 5, 6 to 3. Can you show how they do it in ten jumps?
Solution 217.—THE
TWICKENHAM PUZZLE.
In the illustration we have eleven discs in a circle. On five of the discs we
place white counters with black letters—as shown—and on five other discs the
black counters with white letters. The bottom disc is left vacant. Starting
thus, it is required to get the counters into order so that they spell the word
"Twickenham" in a clockwise direction, leaving the vacant disc in the original
position. The black counters move in the direction that a clock-hand revolves,
and the white counters go the opposite way. A counter may jump over one of the
opposite colour if the vacant disc is next beyond. Thus, if your first move is
with K, then C can jump over K. If then K moves towards E, you may next jump W
over C, and so on. The puzzle may be solved in twenty-six moves. Remember a
counter cannot jump over one of its own colour.
Solution 218.—THE
VICTORIA CROSS PUZZLE.
The puzzle-maker is peculiarly a "snapper-up of unconsidered trifles," and
his productions are often built up with the slenderest materials. Trivialities
that might entirely escape the observation of others, or, if they were observed,
would be regarded as of no possible moment, often supply the man who is in quest
of posers with a pretty theme or an idea that he thinks possesses some "basal
value."
When seated opposite to a lady in a railway carriage at the time of Queen
Victoria's Diamond Jubilee, my attention was attracted to a brooch that she was
wearing. It was in the form of a Maltese or Victoria Cross, and bore the letters
of the word VICTORIA. The number and arrangement of the letters immediately gave
me the suggestion for the puzzle which I now present.
The diagram, it will be seen, is composed of nine divisions. The puzzle is to
place eight counters, bearing the letters of the word VICTORIA, exactly in the
manner shown, and then slide one letter at a time from black to white and white
to black alternately, until the word reads round in the same direction, only
with the initial letter V on one of the black arms of the cross. At no time may
two letters be in the same division. It is required to find the shortest
method.
Leaping moves are, of course, not permitted. The first move must obviously be
made with A, I, T, or R. Supposing you move T to the centre, the next counter
played will be O or C, since I or R cannot be moved. There is something a little
remarkable in the solution of this puzzle which I will explain.
Solution 219.—THE
LETTER BLOCK PUZZLE.
Here is a little reminiscence of our old friend the Fifteen Block Puzzle.
Eight wooden blocks are lettered, and are placed in a box, as shown in the
illustration. It will be seen that you can only move one block at a time to the
place vacant for the time being, as no block may be lifted out of the box. The
puzzle is to shift them about until you get them in the order—
A B C
D E F
G H
This you will find by no means difficult if you are allowed as many moves as
you like. But the puzzle is to do it in the fewest possible moves. I will not
say what this smallest number of moves is, because the reader may like to
discover it for himself. In writing down your moves you will find it necessary
to record no more than the letters in the order that they are shifted. Thus,
your first five moves might be C, H, G, E, F; and this notation can have no
possible ambiguity. In practice you only need eight counters and a simple
diagram on a sheet of paper.
Solution 220.—A
LODGING-HOUSE DIFFICULTY.
The Dobsons secured apartments at Slocomb-on-Sea. There were six rooms on the
same floor, all communicating, as shown in the diagram. The rooms they took were
numbers 4, 5, and 6, all facing the sea. But a little difficulty arose. Mr.
Dobson insisted that the piano and the bookcase should change rooms. This was
wily, for the Dobsons were not musical, but they wanted to prevent any one else
playing the instrument. Now, the rooms were very small and the pieces of
furniture indicated were very big, so that no two of these articles could be got
into any room at the same time. How was the exchange to be made with the least
possible labour? Suppose, for example, you first move the wardrobe into No. 2;
then you can move the bookcase to No. 5 and the piano to No. 6, and so on. It is
a fascinating puzzle, but the landlady had reasons for not appreciating it. Try
to solve her difficulty in the fewest possible removals with counters on a sheet
of paper.
Solution 221.—THE
EIGHT ENGINES.
The diagram represents the engine-yard of a railway company under eccentric
management. The engines are allowed to be stationary only at the nine points
indicated, one of which is at present vacant. It is required to move the
engines, one at a time, from point to point, in seventeen moves, so that their
numbers shall be in numerical order round the circle, with the central point
left vacant. But one of the engines has had its fire drawn, and therefore cannot
move. How is the thing to be done? And which engine remains stationary
throughout?
Solution 222.—A
RAILWAY PUZZLE.
Make a diagram, on a large sheet of paper, like the illustration, and have
three counters marked A, three marked B, and three marked C. It will be seen
that at the intersection of lines there are nine stopping-places, and a tenth
stopping-place is
attached to the outer circle like the tail of a Q. Place the three counters or
engines marked A, the three marked B, and the three marked C at the places
indicated. The puzzle is to move the engines, one at a time, along the lines,
from stopping-place to stopping-place, until you succeed in getting an A, a B,
and a C on each circle, and also A, B, and C on each straight line. You are
required to do this in as few moves as possible. How many moves do you need?
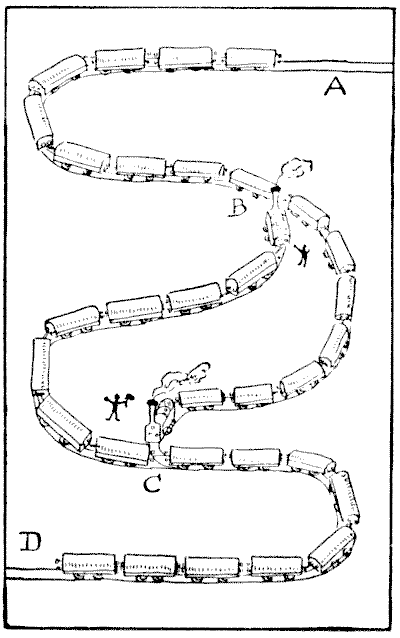
Solution 223.—A
RAILWAY MUDDLE.
The plan represents a portion of the line of the London, Clodville, and
Mudford Railway Company. It is a single line with a loop. There is only room for
eight wagons, or seven wagons and an engine, between B and C on either the left
line or the right line of the loop. It happened that two goods trains (each
consisting of an engine and sixteen wagons) got into the position shown in the
illustration. It looked like a hopeless deadlock, and each engine-driver wanted
the other to go back to the next station and take off nine wagons. But an
ingenious stoker undertook to pass the trains and send them on their respective
journeys with their engines properly in front. He also contrived to reverse the
engines the fewest times possible. Could you have performed the feat? And how
many times would you require to reverse the engines? A "reversal" means a change
of direction, backward or forward. No rope-shunting, fly-shunting, or other
trick is allowed. All the work must be done legitimately by the two engines. It
is a simple but interesting puzzle if attempted with counters.
Solution 224.—THE
MOTOR-GARAGE PUZZLE.
The difficulties of the proprietor of a motor garage are converted into a
little pastime of a kind that has a peculiar fascination. All you need is to
make a simple plan or diagram on a sheet of paper or cardboard and number eight
counters, 1 to 8. Then a whole family can enter into an amusing competition to
find the best possible solution of the difficulty.
The illustration represents the plan of a motor garage, with accommodation
for twelve cars. But the premises are so inconveniently restricted that the
proprietor is often caused considerable perplexity. Suppose, for example, that
the eight cars numbered 1 to 8 are in the positions shown, how are they to be
shifted in the quickest possible way so that 1, 2, 3, and 4 shall change places
with 5, 6, 7, and 8—that is, with the numbers still running from left to right,
as at present, but the top row exchanged with the bottom row? What are the
fewest possible moves?
One car moves at a time, and any distance counts as one move. To prevent
misunderstanding, the stopping-places are marked in squares, and only one car
can be in a square at the same time.
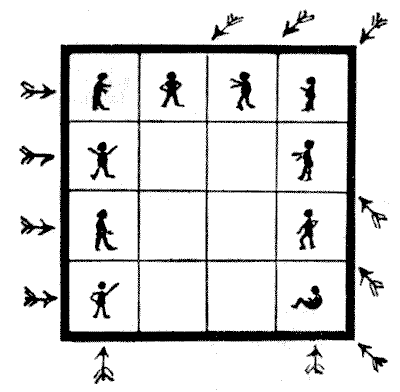
Solution 225.—THE
TEN PRISONERS.
If prisons had no other use, they might still be preserved for the special
benefit of puzzle-makers. They appear to be an inexhaustible mine of perplexing
ideas. Here is a little poser that will perhaps interest the reader for a short
period. We have in the illustration a prison of sixteen cells. The locations of
the ten prisoners will be seen. The jailer has queer superstitions about odd and
even numbers, and he wants to rearrange the ten prisoners so that there shall
be as many even rows of men, vertically, horizontally, and diagonally, as
possible. At present it will be seen, as indicated by the arrows, that there are
only twelve such rows of 2 and 4. I will state at once that the greatest number
of such rows that is possible is sixteen. But the jailer only allows four men to
be removed to other cells, and informs me that, as the man who is seated in the
bottom right-hand corner is infirm, he must not be moved. Now, how are we to get
those sixteen rows of even numbers under such conditions?
Solution 226.—ROUND
THE COAST.
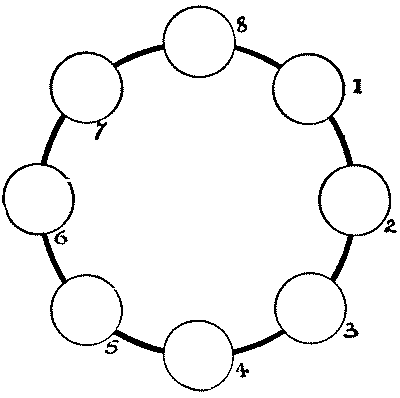
Here is a puzzle that will, I think, be found as amusing as instructive. We
are given a ring of eight circles. Leaving circle 8 blank, we are required to
write in the name of a seven-lettered port in the United Kingdom in this manner.
Touch a blank circle with your pencil, then jump over two circles in either
direction round the ring, and write down the first letter. Then touch another
vacant circle, jump over two circles, and write down your second letter. Proceed
similarly with the other letters in their proper order until you have completed
the word. Thus, suppose we select "Glasgow," and proceed as follows: 6—1, 7—2,
8—3, 7—4, 8—5, which means that we touch 6, jump over 7 and and write down "G"
on 1; then touch 7, jump over 8 and 1, and write down "l" on 2; and so on. It
will be found that after we have written down the first five letters—"Glasg"—as
above, we cannot go any further. Either there is something wrong with "Glasgow,"
or we have not managed our jumps properly. Can you get to the bottom of the
mystery?
Solution 227.—CENTRAL
SOLITAIRE.
This ancient puzzle was a great favourite with our grandmothers, and most of
us, I imagine, have on occasions come across a "Solitaire" board—a round
polished board with holes cut in it in a geometrical pattern, and a glass marble
in every hole. Sometimes I have noticed one on a side table in a suburban front
parlour, or found one on a shelf in a country cottage, or had one brought under
my notice at a wayside inn. Sometimes they are of the form shown above, but it
is equally common for the board to have four more holes, at the points indicated
by dots. I select the simpler form.
Though "Solitaire" boards are still sold at the toy shops, it will be
sufficient if the reader will make an enlarged copy of the above on a sheet of
cardboard or paper, number the "holes," and provide himself with 33 counters,
buttons, or beans. Now place a counter in every hole except the central one, No.
17, and the puzzle is to take off all the counters in a series of jumps, except
the last counter, which must be left in that central hole. You are allowed to jump one
counter over the next one to a vacant hole beyond, just as in the game of
draughts, and the counter jumped over is immediately taken off the board. Only
remember every move must be a jump; consequently you will take off a counter at
each move, and thirty-one single jumps will of course remove all the thirty-one
counters. But compound moves are allowed (as in draughts, again), for so long as
one counter continues to jump, the jumps all count as one move.
Here is the beginning of an imaginary solution which will serve to make the
manner of moving perfectly plain, and show how the solver should write out his
attempts: 5-17, 12-10, 26-12, 24-26 (13-11, 11-25), 9-11 (26-24, 24-10, 10-12),
etc., etc. The jumps contained within brackets count as one move, because they
are made with the same counter. Find the fewest possible moves. Of course, no
diagonal jumps are permitted; you can only jump in the direction of the
lines.
Solution 228.—THE
TEN APPLES.
The family represented in the illustration are amusing themselves with this
little puzzle, which is not very difficult but quite interesting. They have, it
will be seen, placed sixteen plates on the table in the form of a square, and
put an apple in each of ten plates. They want to find a way of removing all the
apples except one by jumping over one at a time to the next vacant square, as in
draughts; or, better, as in solitaire, for you are not allowed to make any
diagonal moves—only moves parallel to the sides of the square. It is obvious
that as the apples stand no move can be made, but you are permitted to transfer
any single apple you like to a vacant plate before starting. Then the moves must
be all leaps, taking off the apples leaped over.
Solution 229.—THE
NINE ALMONDS.
"Here is a little puzzle," said a Parson, "that I have found peculiarly
fascinating. It is so simple, and yet it keeps you interested indefinitely."
The reverend gentleman took a sheet of paper and divided it off into
twenty-five squares, like a square portion of a chessboard. Then he placed nine
almonds on the central squares, as shown in the illustration, where we have
represented numbered counters for convenience in giving the solution.
"Now, the puzzle is," continued the Parson, "to remove eight of the almonds
and leave the ninth in the central square. You make the removals by jumping one
almond over another to the vacant square beyond and taking off the one jumped
over—just as in draughts, only here you can jump in any direction, and not
diagonally only. The point is to do the thing in the fewest possible moves."
The following specimen attempt will make everything clear. Jump 4 over 1, 5
over 9, 3 over 6, 5 over 3, 7 over 5 and 2, 4 over 7, 8 over 4. But 8 is not
left in the central square, as it should be. Remember to remove those you jump over. Any
number of jumps in succession with the same almond count as one move.
Solution 230.—THE
TWELVE PENNIES.
Here is a pretty little puzzle that only requires twelve pennies or counters.
Arrange them in a circle, as shown in the illustration. Now take up one penny at
a time and, passing it over two pennies, place it on the third penny. Then take
up another single penny and do the same thing, and so on, until, in six such
moves, you have the coins in six pairs in the positions 1, 2, 3, 4, 5, 6. You
can move in either direction round the circle at every play, and it does not
matter whether the two jumped over are separate or a pair. This is quite easy if
you use just a little thought.
Solution 231.—PLATES
AND COINS.
Place twelve plates, as shown, on a round table, with a penny or orange in
every plate. Start from any plate you like and, always going in one direction
round the table, take up one penny, pass it over two other pennies, and place it
in the next plate. Go on again; take up another penny and, having passed it over
two pennies, place it in a plate; and so continue your journey. Six coins only
are to be removed, and when these have been placed there should be two coins in
each of six plates and six plates empty. An important point of the puzzle is to
go round the table as few times as possible. It does not matter whether the two
coins passed over are in one or two plates, nor how many empty plates you pass a
coin over. But you must always go in one direction round the table and end at
the point from which you set out. Your hand, that is to say, goes steadily
forward in one direction, without ever moving backwards.
Solution 232.—CATCHING
THE MICE.
"Play fair!" said the mice. "You know the rules of the game."
"Yes, I know the rules," said the cat. "I've got to go round and round the
circle, in the direction that you are looking, and eat every thirteenth
mouse, but I must keep the white mouse for a tit-bit at the finish. Thirteen is
an unlucky number, but I will do my best to oblige you."
"Hurry up, then!" shouted the mice.
"Give a fellow time to think," said the cat. "I don't know which of you to
start at. I must figure it out."
While the cat was working out the puzzle he fell asleep, and, the spell being
thus broken, the mice returned home in safety. At which mouse should the cat
have started the count in order that the white mouse should be the last
eaten?
When the reader has solved that little puzzle, here is a second one for him.
What is the smallest number that the cat can count round and round the circle,
if he must start at the white mouse (calling that "one" in the count) and still
eat the white mouse last of all?
And as a third puzzle try to discover what is the smallest number that the
cat can count round and round if she must start at the white mouse (calling that
"one") and make the white mouse the third eaten.
Solution 233.—THE
ECCENTRIC CHEESEMONGER.

The cheesemonger depicted in the illustration is an inveterate puzzle lover.
One of his favourite puzzles is the piling of cheeses in his warehouse, an
amusement that he finds good exercise for the body as well as for the mind. He
places sixteen cheeses on the floor in a straight row and then makes them into
four piles, with four cheeses in every pile, by always passing a cheese over
four others. If you use sixteen counters and number them in order from 1 to 16,
then you may place 1 on 6, 11 on 1, 7 on 4, and so on, until there are four in
every pile. It will be seen that it does not matter whether the four passed over
are standing alone or piled; they count just the same, and you can always carry
a cheese in either direction. There are a great many different ways of doing it
in twelve moves, so it makes a good game of "patience" to try to solve it so
that the four piles shall be left in different stipulated places. For example,
try to leave the piles at the extreme ends of the row, on Nos. 1, 2, 15 and 16;
this is quite easy. Then try to leave three piles together, on Nos. 13, 14, and
15. Then again play so that they shall be left on Nos. 3, 5, 12, and 14.
Solution 234.—THE
EXCHANGE PUZZLE.
Here is a rather entertaining little puzzle with moving counters. You only
need twelve counters—six of one colour, marked A, C, E, G, I, and K, and the
other six marked B, D, F, H, J, and L. You first place them on the diagram, as
shown in the illustration, and the puzzle is to get them into regular
alphabetical order, as follows:—
The moves are made by exchanges of opposite colours standing on the same
line. Thus, G and J may exchange places, or F and A, but you cannot exchange G
and C, or F and D, because in one case they are both white and in the other case
both black. Can you bring about the required arrangement in seventeen
exchanges?
It cannot be done in fewer moves. The puzzle is really much easier than it
looks, if properly attacked.
Solution 235.—TORPEDO
PRACTICE.
If a fleet of sixteen men-of-war were lying at anchor and surrounded by the
enemy, how many ships might be sunk if every torpedo, projected in a straight
line, passed under three vessels and sank the fourth? In the diagram we have
arranged the fleet in square formation, where it will be seen that as many as
seven ships may be sunk (those in the top row and first column) by firing the
torpedoes indicated by arrows. Anchoring the fleet as we like, to what extent
can we increase this number? Remember that each successive ship is sunk before
another torpedo is launched, and that every torpedo proceeds in a different
direction; otherwise, by placing the ships in a straight line, we might sink as
many as thirteen! It is an interesting little study in naval warfare, and
eminently practical—provided the enemy will allow you to arrange his fleet for
your convenience and promise to lie still and do nothing!
Solution 236.—THE
HAT PUZZLE.
Ten hats were hung on pegs as shown in the illustration—five silk hats and
five felt "bowlers," alternately silk and felt. The two pegs at the end of the
row were empty.
The puzzle is to remove two contiguous hats to the vacant pegs, then two
other adjoining hats to the pegs now unoccupied, and so on until five pairs have
been moved and the hats again hang in an unbroken row, but with all the silk
ones together and all the felt hats together.
Remember, the two hats removed must always be contiguous ones, and you must
take one in each hand and place them on their new pegs without reversing their
relative position. You are not allowed to cross your hands, nor to hang up one
at a time.
Can you solve this old puzzle, which I give as introductory to the next? Try
it with counters of two colours or with coins, and remember that the two empty
pegs must be left at one end of the row.
Solution 237.—BOYS
AND GIRLS.
If you mark off ten divisions on a sheet of paper to represent the chairs,
and use eight numbered counters for the children, you will have a fascinating
pastime. Let the odd numbers represent boys and even numbers girls, or you can
use counters of two colours, or coins.
The puzzle is to remove two children who are occupying adjoining chairs and
place them in two empty chairs, making them first change sides; then
remove a second pair of children from adjoining chairs and place them in the two
now vacant, making them change sides; and so on, until all the boys are together
and all the girls together, with the two vacant chairs at one end as at present.
To solve the puzzle you must do this in five moves. The two children must always
be taken from chairs that are next to one another; and remember the important
point of making the two children change sides, as this latter is the distinctive feature of
the puzzle. By "change sides" I simply mean that if, for example, you first move
1 and 2 to the vacant chairs, then the first (the outside) chair will be
occupied by 2 and the second one by 1.
Solution 238.—ARRANGING
THE JAMPOTS.
I happened to see a little girl sorting out some jam in a cupboard for her
mother. She was putting each different kind of preserve apart on the shelves. I
noticed that she took a pot of damson in one hand and a pot of gooseberry in the
other and made them change places; then she changed a strawberry with a
raspberry, and so on. It was interesting to observe what a lot of unnecessary
trouble she gave herself by making more interchanges than there was any need
for, and I thought it would work into a good puzzle.

It will be seen in the illustration that little Dorothy has to manipulate
twenty-four large jampots in as many pigeon-holes. She wants to get them in
correct numerical order—that is, 1, 2, 3, 4, 5, 6 on the top shelf, 7, 8, 9, 10,
11, 12 on the next shelf, and so on. Now, if she always takes one pot in the
right hand and another in the left and makes them change places, how many of
these interchanges will be necessary to get all the jampots in proper order? She
would naturally first change the 1 and the 3, then the 2 and the 3, when she
would have the first three pots in their places. How would you advise her to go
on then? Place some numbered counters on a sheet of paper divided into squares
for the pigeon-holes, and you will find it an amusing puzzle.
Solution
Previous Next
|